만족
[알고리즘] 세그먼트 트리(Segment Tree) 본문
[알고리즘] 세그먼트 트리(Segment Tree)
기타 CS 이론/Algorithm Satisfaction 2021. 11. 30. 03:25문제
길이가 4인 [1,2,3,4] 배열이 있다.
여기에서 인덱스 0번부터 2번까지의 합을 구하라.
또, 인덱스 1번의 값을 10으로 변경했을 때의 인덱스 0번부터 2번까지의 합을 구해보라.
생각해볼 것
가장 간단한 방법은 주어진 범위(0~2)까지 배열을 순회하며 합계값을 구할 수 있다.
중간에 값이 바뀌면, 배열의 해당 인덱스의 값을 바꾼 후,
다시 주어진 범위에 대해 순회하며 합계값을 구할수 있다.
그러나 여기서 배열의 길이가 4가 아니라, 천만으로 증가하고
구간이 0~500만, 200만~700만, ... (구간의 길이가 500만)처럼 구해야 하는 누적합의 종류가 100가지라고 해보자.
이렇게 되면 매 구간에 해당하는 인덱스 위치를 모두 순회하여 부분합을 새로 계산해야 하므로
구간의 길이인 500만에 누적합의 종류의 갯수가 100가지이므로 5000만번 탐색해야 한다.
즉 계산해야 하는 범위가 다양할 때 매번 범위의 누적합을 새로 계산하는 것은 비효율적이라는 것을 의미한다.
세그먼트 트리를 이용한 부분합 구하기: 1- 세그먼트 트리 생성
세그먼트 트리를 구하면 매번 주어진 범위의 인덱스를 순회하며 누적값을 구하지 않아도 된다.
[1,2,3,4]의 배열에 대해 세그먼트 트리를 만들면 형태는 다음과 같다.
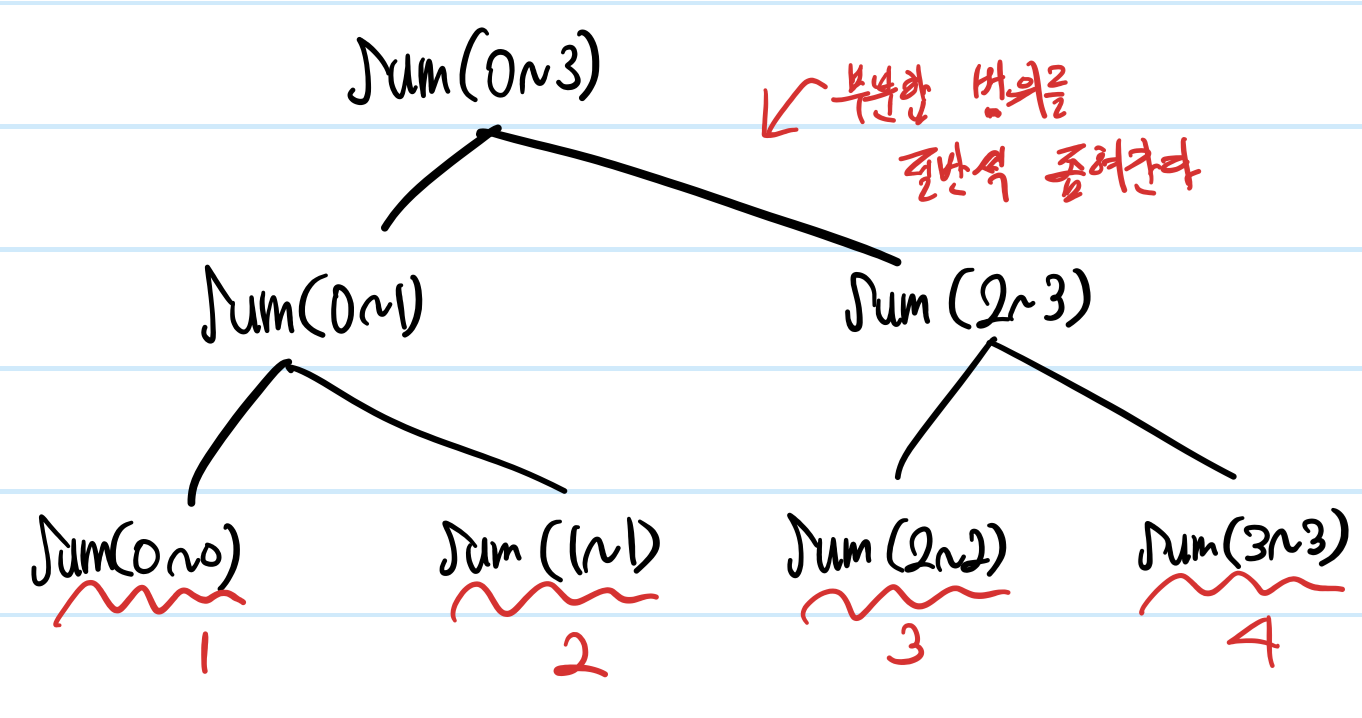
맨 아래쪽 노드(리프 노드) 는 배열의 원소의 값이 직접 들어간다.
세그먼트 트리의 루트(sum(0~3))는 0~3, 즉 주어진 배열의 모든 원소의 합의 값이 들어간다.
루트 노드의 왼쪽 노드는 0~1 인덱스 위치의 값들의 합이고
루트 노드의 오른쪽 노드는 2~3인덱스 위치의 값들의 합이다.
다시 0~1인덱스 위치의 값들의 합 노드의 자식은 0, 1로 쪼개지며
더 이상 자식을 만들어낼 수 없으므로(1개 값에 대한 부분합 생성 불가)
0번째 위치의 원소의 값(1)과 1번째 위치의 원소의 값(2)가 들어간다.
2~3인덱스 위치의 값들도 마찬가지로 구성한다.

세그먼트 '트리'라고 했지만 실제로 사용할 때는 배열 형태로 이용하고, 접근할 때 트리처럼 접근한다.
여기서 각각의 세그먼트 트리의 노드들은 nodeId값을 갖는데,
편의성을 위해 세그먼트 트리 배열의 0번 인덱스는 사용하지 않고 루트 노드를 id= 1부터 시작한다
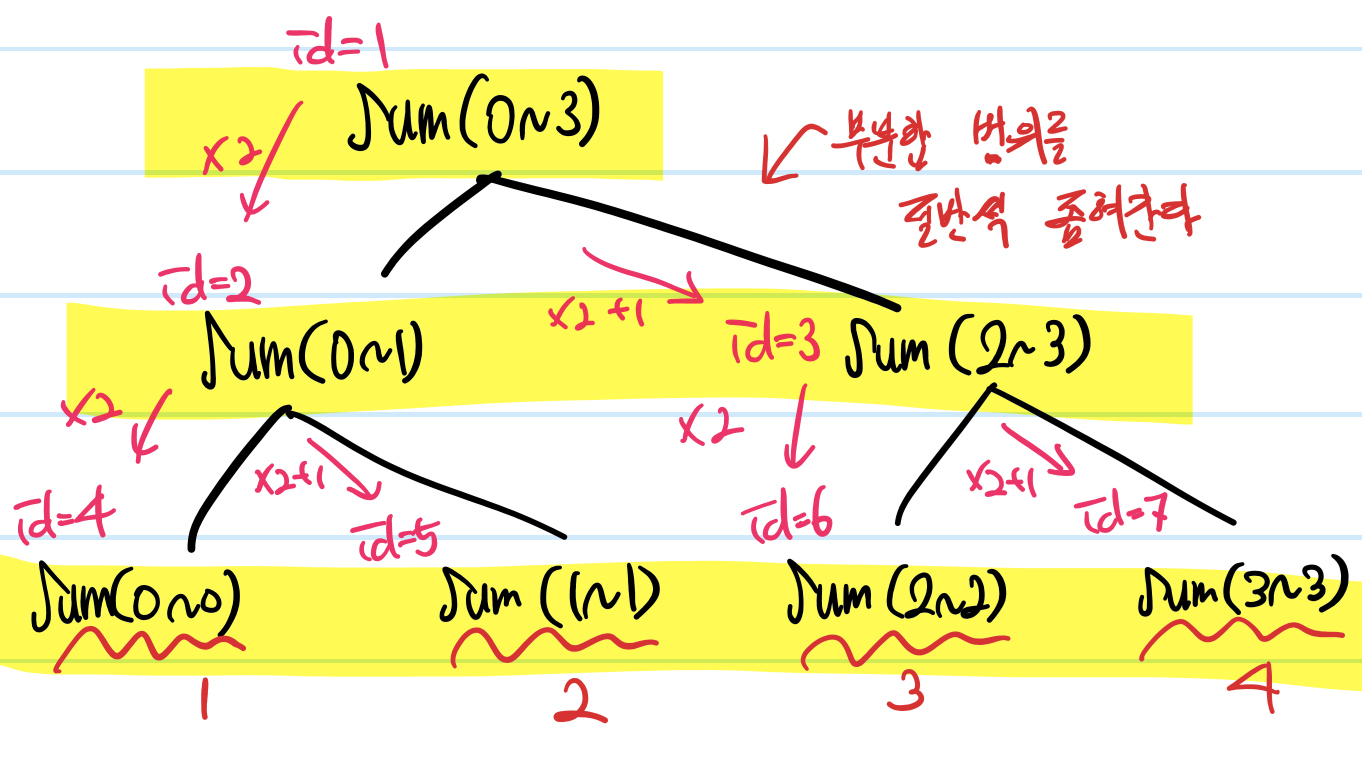
다시 세그먼트 트리로 돌아와서,
핑크색으로 표기한 값이 세그먼트 트리 노드의 nodeId이다.
루트 노드(sum(0~3))가 1, 그리고 루트의 왼쪽 자식(sum(0~1))이 2이고 오른쪽 자식(sum(2~3))이 3이다.
이렇게 트리의 깊이가 한 단계씩 깊어질 때 마다 nodeId는
부모 노드의 nodeId값의 두배(왼쪽 자식), nodeId값의 두배+ 1(오른쪽 자식)의 값이 된다.

이제 세그먼트 트리를 배열로 표현했을 때 왜 이런 순서로 표기되었는지 이해할 수 있다.
코드로 표현하면 아래와 같다.
const input = [1, 2, 3, 4];
const segmentTree = [];
const createSegmentTree = () => {
const init = (nodeId=1, left, right) => {
if (left === right) {
//범위가 아닌 단일 값까지 조여졌을 경우 그냥 현재 인덱스의 원소값을 노드에 입력
return segmentTree[nodeId] = input[left];
}
//주어진 left~right 범위를 반으로 자름
let mid = Math.floor((left + right) / 2);
//왼쪽 자식의 nodeId는 *2
let leftVal = init(nodeId * 2, left, mid);
//오른쪽 자식의 nodeId는 *2+1
let rightVal = init(nodeId * 2 + 1, mid + 1, right);
//현재 노드의 값은 왼쪽 자식의 값+ 오른쪽 자식의 값
return segmentTree[nodeId]= leftVal + rightVal;
}
init(1, 0, input.length - 1);
}
createSegmentTree();
console.log('세그먼트 트리 초기화 완료', segmentTree);세그먼트 트리 초기화 완료 [ 0, 10, 3, 7, 1, 2, 3, 4 ]
실행시키면 위와 같이 세그먼트 트리의 각 노드들이 지정된 범위의 합계값을 저장하고 있다.
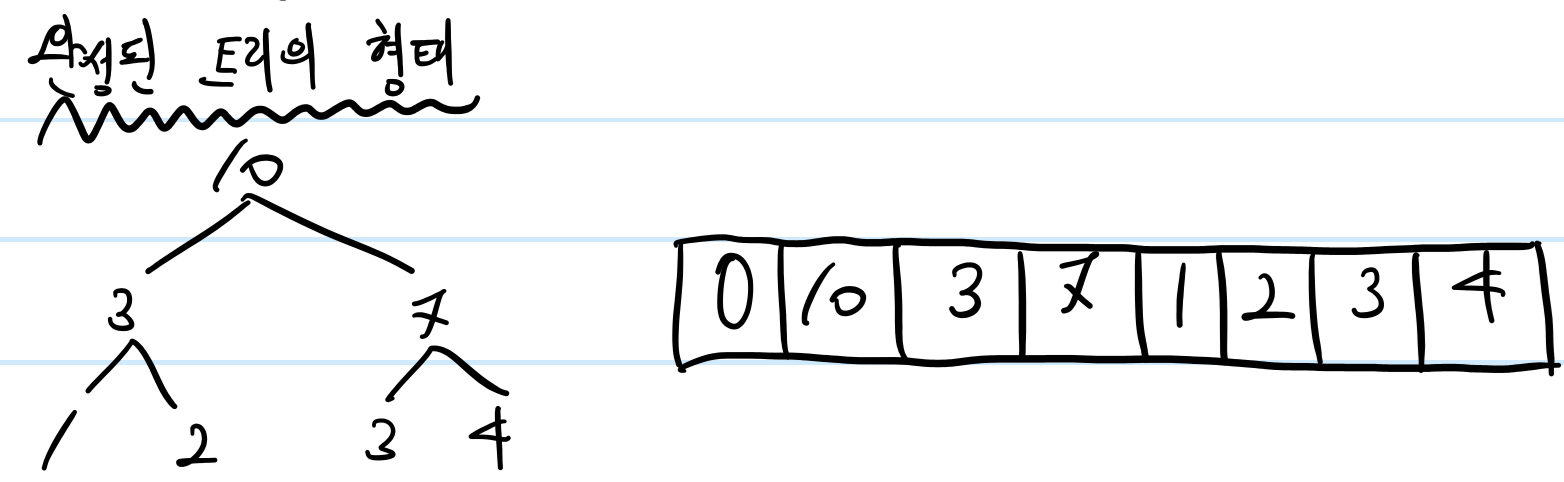
세그먼트 트리를 이용한 부분합 구하기: 2- 세그먼트 트리에서 원하는 범위의 누적합 구하기
세그먼트 트리를 만들었으니, 이 만들어진 트리를 이용해 원하는 범위의 누적합을 구해보자.
[0~2]번 인덱스의 원소(1+2+3)의 누적합을 찾아보자.
여기에서도 범위를 절반씩 줄여가며 탐색할텐데,
현재 위치의 노드가 나타내는 부분합의 범위가 내가 원하는 범위 내에 속할 경우는 그 노드의 값을 결과값에 더하고
완전히 범위를 벗어날 경우 더하지 않는다.
만약 범위가 걸쳐있을 경우(현재 노드의 범위가 [2~3]이고 내가 원하는 부분합의 범위가 [0~2]일때,
한칸 더 내려가 범위를 벗어난 노드를 찾으면 0으로 취급하면서(해당 값은 무시하기 위해) 누적합을 구한다.

1. 루트 노드(sum(0~3))은 누적합의 범위가 찾으려는 범위보다 넓으므로, 자식 노드로 이동한다.
2. 루트 노드의 왼쪽 자식(sum(0~1))은 누적합의 범위가 찾으려는 범위에 완전히 포함되므로 값을 리턴한다.
3. 루트 노드의 오른쪽 자식(sum(2~3))은 누적합의 범위가 찾으려는 범위보다 넓으므로, 자식 노드로 이동한다.
4. sum(2~3)의 왼쪽 자식은 3(=sum(2~2)이고 범위 2~2는 찾으려는 범위에 포함되므로 값을 리턴한다.
5. sum(2~3)의 오른쪽 자식은 4(=sum(3~3)이고 범위 3~3은 찾으려는 범위에 포함되지 않으므로 0을 리턴한다.
이 작업이 끝나면 다음과 같은 형태로 부분합이 구해진다.
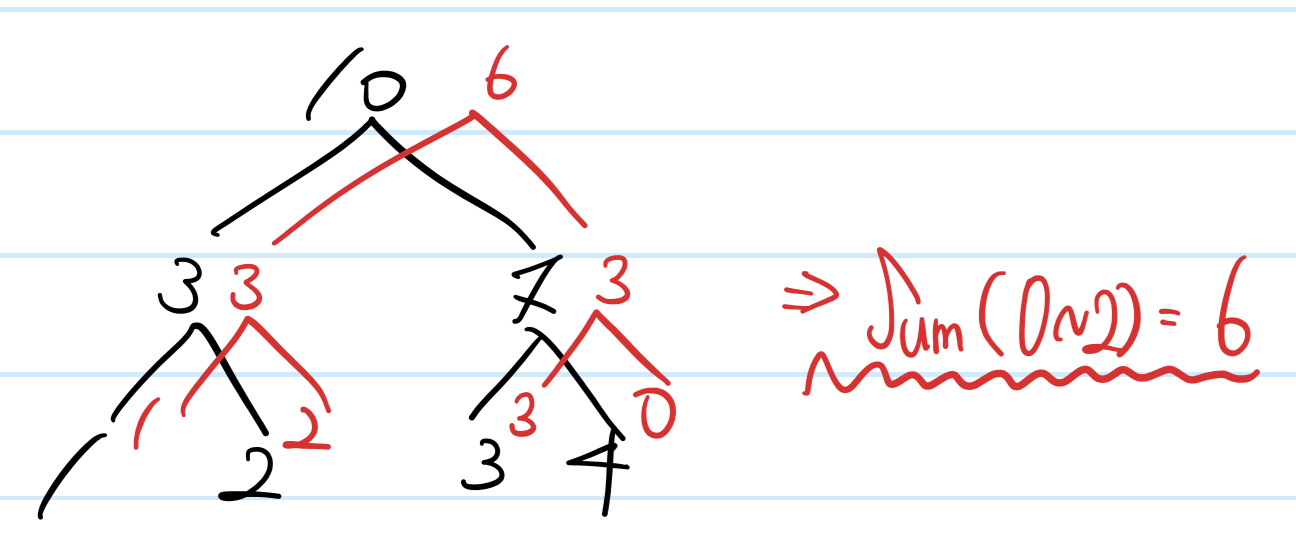
이런 방법으로 0~2번째 인덱스 값들의 합을 구할 수 있다.
코드로 표현하면 다음과 같다.
const input = [1, 2, 3, 4];
const segmentTree = [];
const createSegmentTree = () => {
const init = (nodeId=1, left, right) => {
if (left === right) {
//범위가 아닌 단일 값까지 조여졌을 경우 그냥 현재 인덱스의 원소값을 노드에 입력
return segmentTree[nodeId] = input[left];
}
//주어진 left~right 범위를 반으로 자름
let mid = Math.floor((left + right) / 2);
//왼쪽 자식의 nodeId는 *2
let leftVal = init(nodeId * 2, left, mid);
//오른쪽 자식의 nodeId는 *2+1
let rightVal = init(nodeId * 2 + 1, mid + 1, right);
//현재 노드의 값은 왼쪽 자식의 값+ 오른쪽 자식의 값
return segmentTree[nodeId]= leftVal + rightVal;
}
init(1, 0, input.length - 1);
}
createSegmentTree();
//추가된 부분
const findSubsetSummary = (left, right, nodeId= 1, nodeLeft, nodeRight) => {
if (nodeRight < left || nodeLeft > right) {
//현재 노드의 부분합 범위가 원하는 범위를 벗어남
//무시
return 0;
}
if (left <= nodeLeft && right >= nodeRight) {
//현재 노드의 부분합 범위가 원하는 범위 내에 있음
return segmentTree[nodeId];
}
//현재 노드의 부분합 범위 일부가 원하는 범위에 일부 걸쳐져 있음
let mid = Math.floor((nodeLeft + nodeRight) / 2);
let lval = findSubsetSummary(left, right, nodeId * 2, nodeLeft, mid);
let rval = findSubsetSummary(left, right, nodeId * 2 + 1, mid + 1, nodeRight);
return lval + rval;
}
console.log('세그먼트 트리 초기화 완료', segmentTree);
console.log('0~2번쨰 인덱스 값들의 합은?>> ' ,findSubsetSummary(0, 2, 1, 0, input.length-1))
세그먼트 트리 초기화 완료 [ <1 empty item>, 10, 3, 7, 1, 2, 3, 4 ]
0~2번쨰 인덱스 값들의 합은?>> 6
세그먼트 트리를 이용한 부분합 구하기: 3- 특정 위치의 값 변경 (업데이트)
만약 [1,2,3,4]에서 1번 인덱스(값=2)의 값을 10으로 변경하고,
다시 0~2까지의 합을 구하려고 한다.
선형적인 방법에서는 input[1]= 2를 한 다음 다시 0~2까지 순회하며 합을 구할 것이다.
그러나 세그먼트 트리에서는 적절한 노드의 값만 바꿔줌으로써 걸리는 시간이 O(N)보다 작아지게 된다.

우리는 인덱스 1번의 값을 변경할 것이므로 sum(1~1)위치의 값을 변경시키면서
sum(1~1)과 연관이 있는 노드, 즉 sum(0~1), sum(0~3)의 값을 업데이트하기만 하면 된다.
(어차피 나머지 노드들은 1번 인덱스 위치의 원소 값과 관계없이 값은 동일하다)
(ex: 1번 인덱스의 값이 변경되도 2~3번 인덱스 위치의 원소의 값은 동일하다)
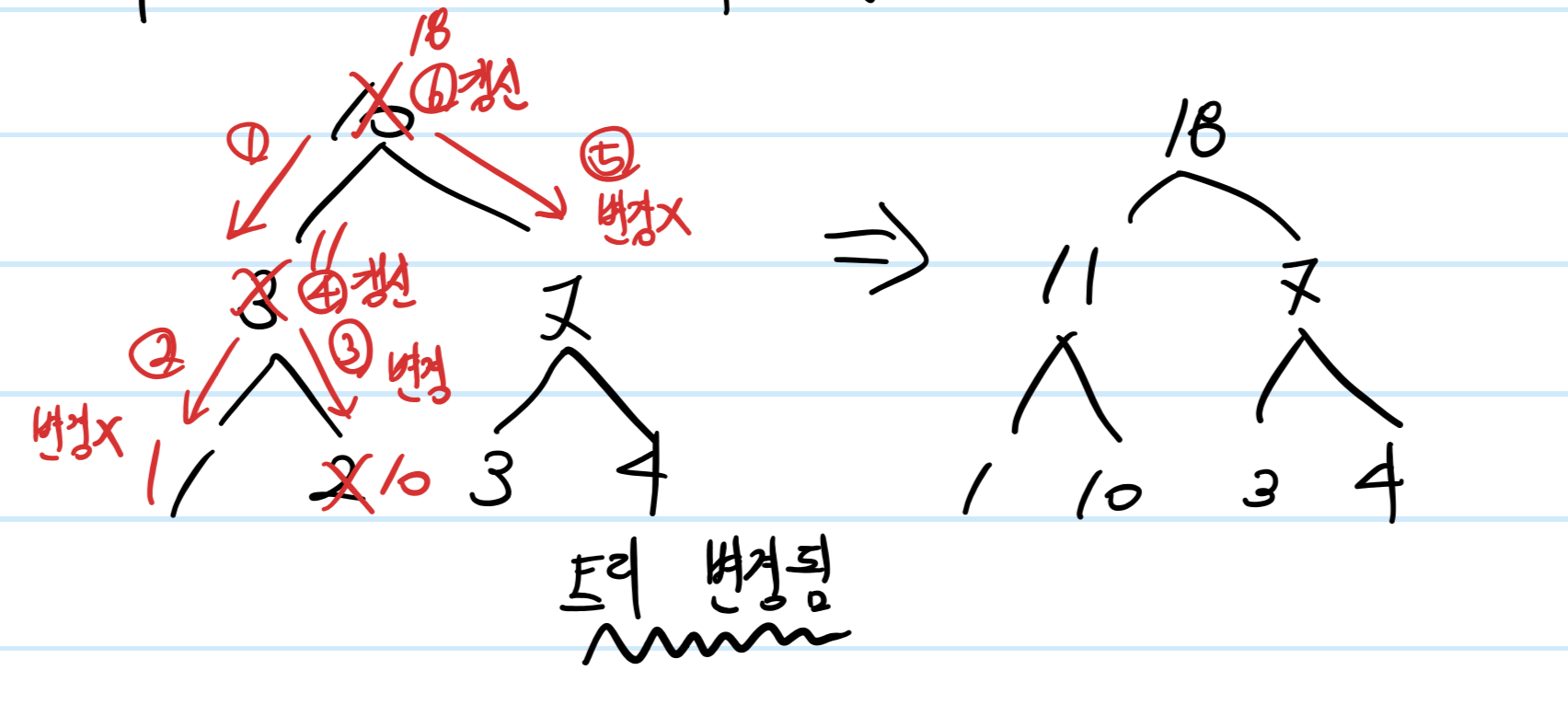
다시 루트 노드(nodeId=1, 세그먼트 트리의 1번 인덱스)부터 시작해서 1번 인덱스가 영향을 주는 노드인지를 판별하여 트리의 값을 업데이트한다.
1. 루트 노드의 범위 0~3은 변경하고자 하는 인덱스의 범위에 영향을 받으므로 자식 노드도 판별한다.
2. 루트의 왼쪽 자식(sum(0~1))의 볌위는 0~1로 변경하고자 하는 인덱스의 범위에 영향을 받으므로 자식 노드도 판별한다.
3. sum(0~1)의 왼쪽 자식의 범위는 0~0으로 영향을 받지 않으므로 갱신하지 않고 자신의 값(1)을 리턴한다.
4. sum(0~1)의 오른쪽 자식의 범위는 1~1으로 영향을 받으므로 값을 갱신하고 그 값(10)을 리턴한다.
5. 루트의 왼쪽 자식 값을 과정 3,4가 리턴한 값을 더해 갱신한다.
6. 루트의 오른쪽 자식(sum(2~3))의 범위는 2~3으로 변경하고자 하는 인덱스의 범위에 영향을 받지 않으므로 자신의 값(7)을 리턴한다.
7. 루트의 값을 왼쪽 자식 값(11)과 오른쪽 자식 값(7)을 더해 갱신한다.
이제 세그먼트 트리가 갱신되었다.
따라서 특정 위치의 값이 변경되어도 처음부터 그 범위를 다시 탐색할 필요가 사라진 것이다.
(마찬가지로 2- 원하는 범위의 값 구하기 방법을 사용해 부분합을 손쉽게 구할 수 있다)
코드는 다음과 같다.
const input = [1, 2, 3, 4];
const segmentTree = [];
const createSegmentTree = () => {
const init = (nodeId=1, left, right) => {
if (left === right) {
//범위가 아닌 단일 값까지 조여졌을 경우 그냥 현재 인덱스의 원소값을 노드에 입력
return segmentTree[nodeId] = input[left];
}
//주어진 left~right 범위를 반으로 자름
let mid = Math.floor((left + right) / 2);
//왼쪽 자식의 nodeId는 *2
let leftVal = init(nodeId * 2, left, mid);
//오른쪽 자식의 nodeId는 *2+1
let rightVal = init(nodeId * 2 + 1, mid + 1, right);
//현재 노드의 값은 왼쪽 자식의 값+ 오른쪽 자식의 값
return segmentTree[nodeId]= leftVal + rightVal;
}
init(1, 0, input.length - 1);
}
createSegmentTree();
const findSubsetSummary = (left, right, nodeId= 1, nodeLeft, nodeRight) => {
if (nodeRight < left || nodeLeft > right) {
//현재 노드의 부분합 범위가 원하는 범위를 벗어남
//무시
return 0;
}
if (left <= nodeLeft && right >= nodeRight) {
//현재 노드의 부분합 범위가 원하는 범위 내에 있음
return segmentTree[nodeId];
}
//현재 노드의 부분합 범위 일부가 원하는 범위에 일부 걸쳐져 있음
let mid = Math.floor((nodeLeft + nodeRight) / 2);
let lval = findSubsetSummary(left, right, nodeId * 2, nodeLeft, mid);
let rval = findSubsetSummary(left, right, nodeId * 2 + 1, mid + 1, nodeRight);
return lval + rval;
}
const updateSegmetTree = (targetIndex, value, nodeId=1, nodeLeft, nodeRight) => {
if (nodeLeft > targetIndex || nodeRight < targetIndex) {
//해당 위치의 노드는 변경될 필요가 없음
return segmentTree[nodeId];
}
if (nodeLeft === nodeRight) {
//변경할 노드 찾음
return segmentTree[nodeId] = value;
}
//왼쪽, 오른쪽 자식에 대해 변경해야 하는지 검사
let mid = Math.floor((nodeLeft + nodeRight) / 2);
let lval = updateSegmetTree(targetIndex, value, nodeId * 2, nodeLeft, mid);
let rval = updateSegmetTree(targetIndex, value, nodeId * 2 + 1, mid + 1, nodeRight);
return segmentTree[nodeId]= lval + rval;
}
console.log('세그먼트 트리 초기화 완료', segmentTree);
console.log('0~2번쨰 인덱스 값들의 합은?>> ', findSubsetSummary(0, 2, 1, 0, input.length - 1));
console.log('1번 인덱스 위치의 값을 10으로 변경', updateSegmetTree(1, 10, 1, 0, input.length - 1));
console.log('업데이트된 세그먼트 트리', segmentTree);
console.log('0~2번쨰 인덱스 값들의 합은?>> ', findSubsetSummary(0, 2, 1, 0, input.length - 1));
세그먼트 트리 초기화 완료 [ <1 empty item>, 10, 3, 7, 1, 2, 3, 4 ]
0~2번쨰 인덱스 값들의 합은?>> 6
1번 인덱스 위치의 값을 10으로 변경 18
업데이트된 세그먼트 트리 [ <1 empty item>, 18, 11, 7, 1, 10, 3, 4 ]
0~2번쨰 인덱스 값들의 합은?>> 14
세그먼트 트리를 이용한 부분합 계산 시 시간복잡도
주어진 배열의 길이를 N이라고 했을 때,
세그먼트 트리를 만들어낼 때 트리의 크기가 4N을 넘어가지 않는다.
(세그먼트 트리를 처음 생성할 때 O(N)만큼의 시간이 걸리기는 하지만 딱 한번 시행하므로,
세그먼트 트리를 이용해 부분합을 구하는 횟수가 증가함에 따라 무시할 수 있다)
또 세그먼트 트리에서 부분합을 구하기 위해 트리를 탐색할 때 이분 탐색을 시행하므로
logN (+C; C는 범위에 걸쳐져 있는 노드의 가짓수)만큼의 시간이 걸린다.
구해야 하는 누적합의 범위 갯수가 M개일 때
세그먼트 트리를 이용한 M번의 부분합 계산은 O(MlogN)의 시간복잡도를 갖는다.
세그먼트 트리를 사용하지 않고 매번 누적합의 범위에 대해 순차탐색을 통해 누적값을 구할 때 O(MN)만큼의 시간이 걸리는 것과 비교하면
매우 빠른 속도를 자랑한다.
'기타 CS 이론 > Algorithm' 카테고리의 다른 글
| [알고리즘] 버블 정렬 (Bubble Sort) (0) | 2021.07.24 |
|---|---|
| [알고리즘] 점근적 표기법 (0) | 2018.11.13 |
| [알고리즘] 이분 탐색(Binaray Search) (3) | 2018.01.16 |
| [알고리즘] 퀵 정렬 (Quick Sort) (0) | 2018.01.15 |
| [알고리즘] 병합 정렬(Merge Sort) (0) | 2018.01.14 |
