만족
[데이터사이언스] Gradient Desent (경사하강법) 본문
[데이터사이언스] Gradient Desent (경사하강법)
데이터사이언스 Satisfaction 2021. 12. 17. 16:49Gradient Desent (경사 하강법)
경사 하강법은 cost의 변화량에 따라 파라미터를 움직여가며
cost가 최소가 되는 지점을 찾는 방법이다.

J(w)를 cost를 계산하는 함수라고 했을 때,
우리는 J(cost)가 최소가 되면서 변화량이 최소가 되는 지점을 찾고 싶다.
J가 최소가 되면서 변화량(미분계수)가 최소가 되는 지점을 찾을 때,
w값을 움직여가면서 J'(w)의 값이 양수이면 J(w)가 커지고 있다는 뜻이므로 파라미터를 반대 방향으로 움직인다.
=> parameter의 변화에 따라 cost가 커지고 있으면 그 변화의 반대 방향으로 움직여야만 cost가 작아진다
반대로 J'(w) 값이 음수이면, cost가 줄어들고 있다는 뜻이므로 파라미터를 정방향으로 움직인다.
경사하강법: 사용
J의 변화량에 따라 어떤 방향으로 파라미터를 움직여야 하는지는 알았지만,
어떻게 그 변화량을 계산해낼 수 있을지는 모른다.
1차함수만 하더라도 계산해야 하는 파라미터(y= ax+ b에서 a,b)는 2개다.
따라서 우리는 각 파라미터에 대한 J의 변화량을 알기 위해 편미분을 사용할 것이다.
y= ax+b에서 cost함수 J는 다음으로 정의된다.

파라미터 a,b에 대해 J를 편미분하면 다음과 같다.

계산된 각 편미분값을 학습계수(learning rate)만큼 곱하고,
이전에 계산된 파라미터값에 더하거나 빼는 것을 반복한다.
언제까지? 각 편미분값이 모두 우리가 미리 정한 임계값에 다다를때까지
파이썬에서 경사하강법 해보기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import pymysql
def gen_dataset():
X= np.random.rand(30, 1)
X= X- 0.5
X= X*10
y= X
return X, y
X, y= gen_dataset()
# plt.show()
#SIMPLE LINEAR REGRESSION : LS
# y= mx+ c에서 적절한 m과 c를 구한다
mc_history= []
#경사하강법 (병렬화 O)
def gradient_descent_vectorized(X, y):
epochs= 100_000
min_grad= 0.0001
learning_rate= 0.001
m= 0
c= 0
n= len(y)
c_grad= 0.0
m_grad= 0.0
for epoch in range(epochs):
y_pred= m* X+ c
m_grad= (2* ((y_pred-y)* X).sum())/n
c_grad= (2* (y_pred-y).sum())/n
# 구해진 grad에 마이너스를 취하는 이유?
# grad<0일 때 0에 가까워지기 위해서는 기울기가 커져야 하고
# grad>0 일 때는 기울기가 작아져야 하기 때문이다
m= m- learning_rate* m_grad
c= c- learning_rate* c_grad
if(True):
mc_history.append([m,c])
if(epoch% 5== 0):
print("epoch: %d ======= " %(epoch))
print("m_grad %f, c_grad: %f, m=%f, c=%f " %(m_grad, c_grad, m, c))
if(abs(m_grad)< min_grad and abs(c_grad)< min_grad):
break
return m, c
import time
start_time= time.time()
gd_m, gd_c= gradient_descent_vectorized(X, y)
end_time= time.time()
print("Vectorized- GD time (s): ", end_time- start_time)
print("\n===== result ====")
print("gd: m=%f, c=%f" %(gd_m, gd_c))
# First set up the figure, the axis, and the plot element we want to animate
fig = plt.figure()
ax = plt.axes()
ax.scatter(X,y)
line, = ax.plot([], [], lw=2, color='red')
# initialization function: plot the background of each frame
def init():
line.set_data([], [])
return line,
# animation function. This is called sequentially
def animate(i):
m,c = mc_history[i% len(mc_history)]
x= np.arange(-10,10)
y= m* x+ c
line.set_data(x,y)
return line,
# call the animator. blit=True means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=60, interval=50, blit=True)
plt.show()
def gradient_desent_vectorized() 에서 y=ax+b (mx+c) 에 대해 경사하강법을 구현하고 있다.
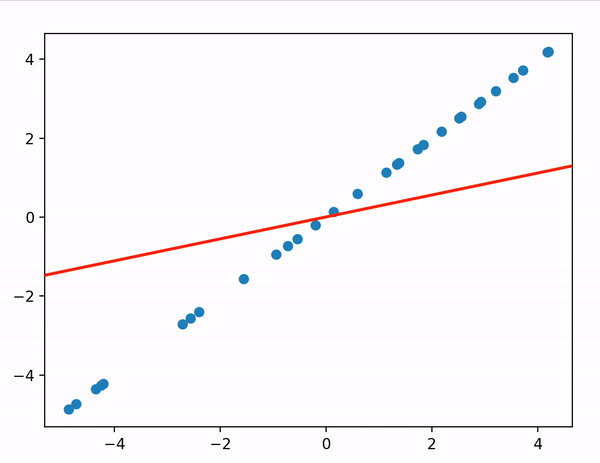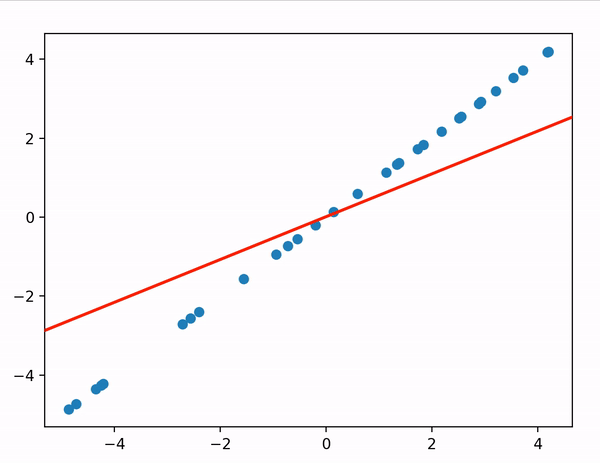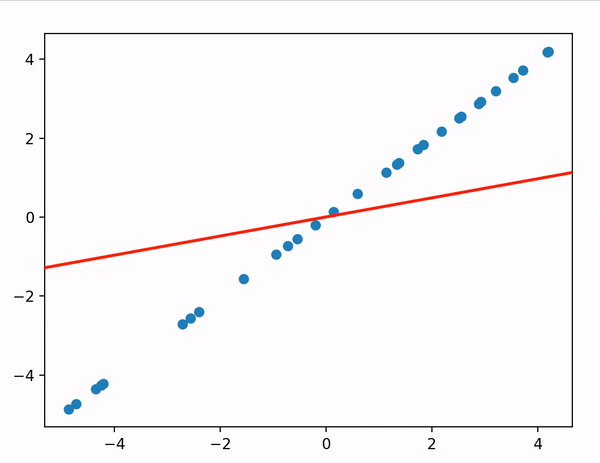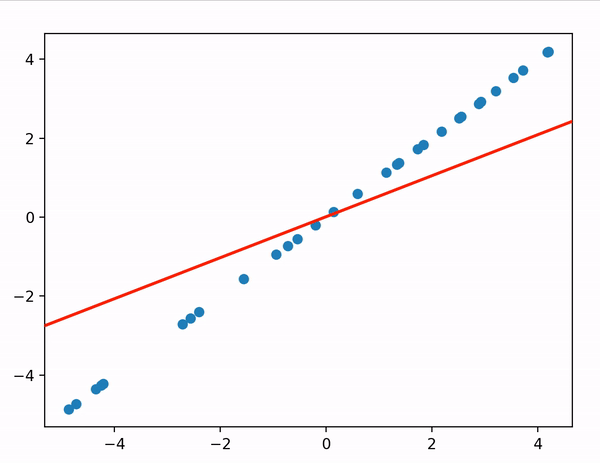
결과는 위처럼 cost함수 J에 대해 파라미터를 조정해가며
cost가 최소가 되는 지점으로 서서히 다가가는 모습을 확인할 수 있다.
실제 y= x로 정의되어 있고(a=1, b=0),
경사하강법이 끝나고 난 후 a=0.99999, b= 0.00005가 되었다.
경사하강법의 한계
대표적인 문제점으로는 global minimum이 아닌 local minimum에 빠질 수 있다는 것이다.
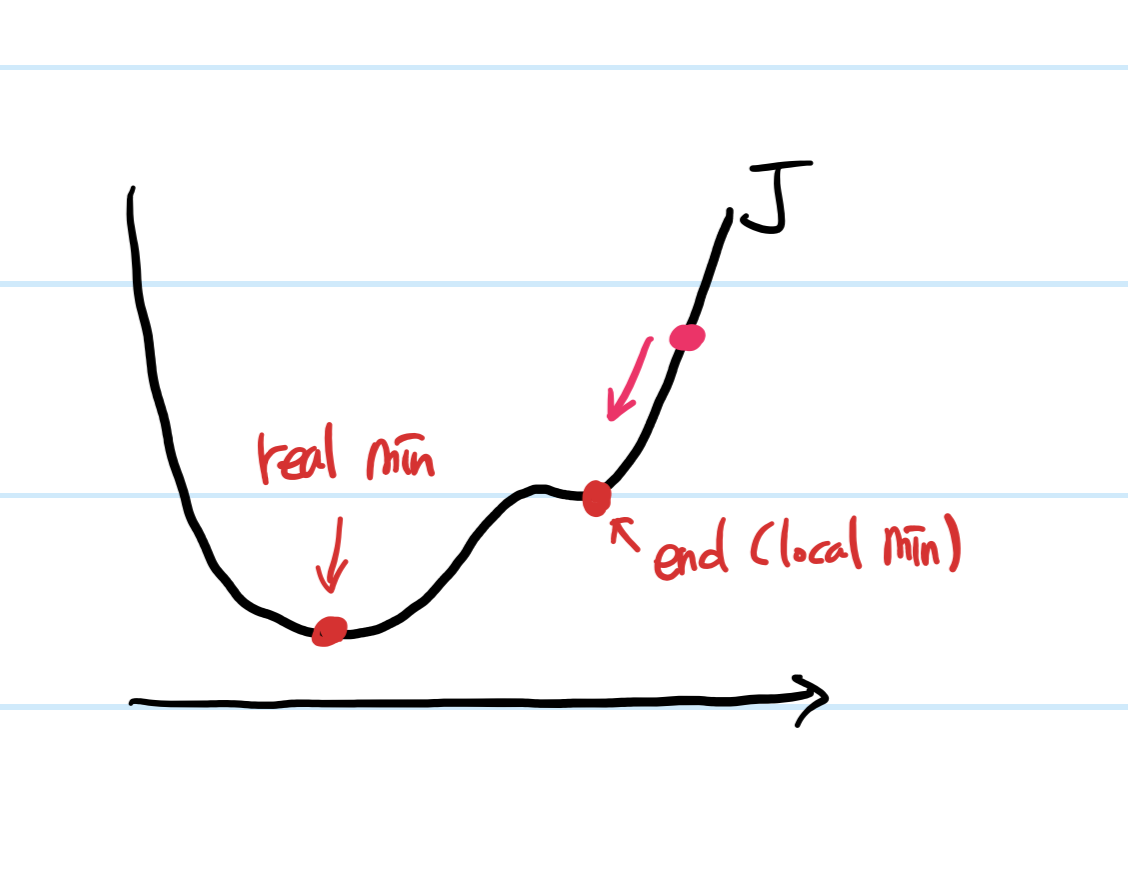
핑크색 지점에서 탐색을 시작했을 경우,
end지점에서 변화량이 급격히 작아져서 실제 최소값에 다다르기 전에 탐색이 끝난다.
즉 경사하강법은 탐색 시작 위치에 따라 실제 최소값이 아닌,
특정 구간에서의 최소값을 기준으로 매개변수가 결정될 수 있다는 문제점이 있다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] Neural Network (뉴럴 네트워크) (0) | 2021.12.17 |
|---|---|
| [데이터사이언스] Logistic Regression (0) | 2021.12.17 |
| [데이터사이언스] Regression Performance Estimation (회귀 성능 평가) (0) | 2021.10.22 |
| [데이터사이언스] Regression (회귀) (0) | 2021.10.22 |
| [데이터사이언스] 머신러닝 개요 (0) | 2021.10.22 |




