만족
[데이터사이언스] Neural Network (뉴럴 네트워크) 본문
[데이터사이언스] Neural Network (뉴럴 네트워크)
데이터사이언스 Satisfaction 2021. 12. 17. 18:27
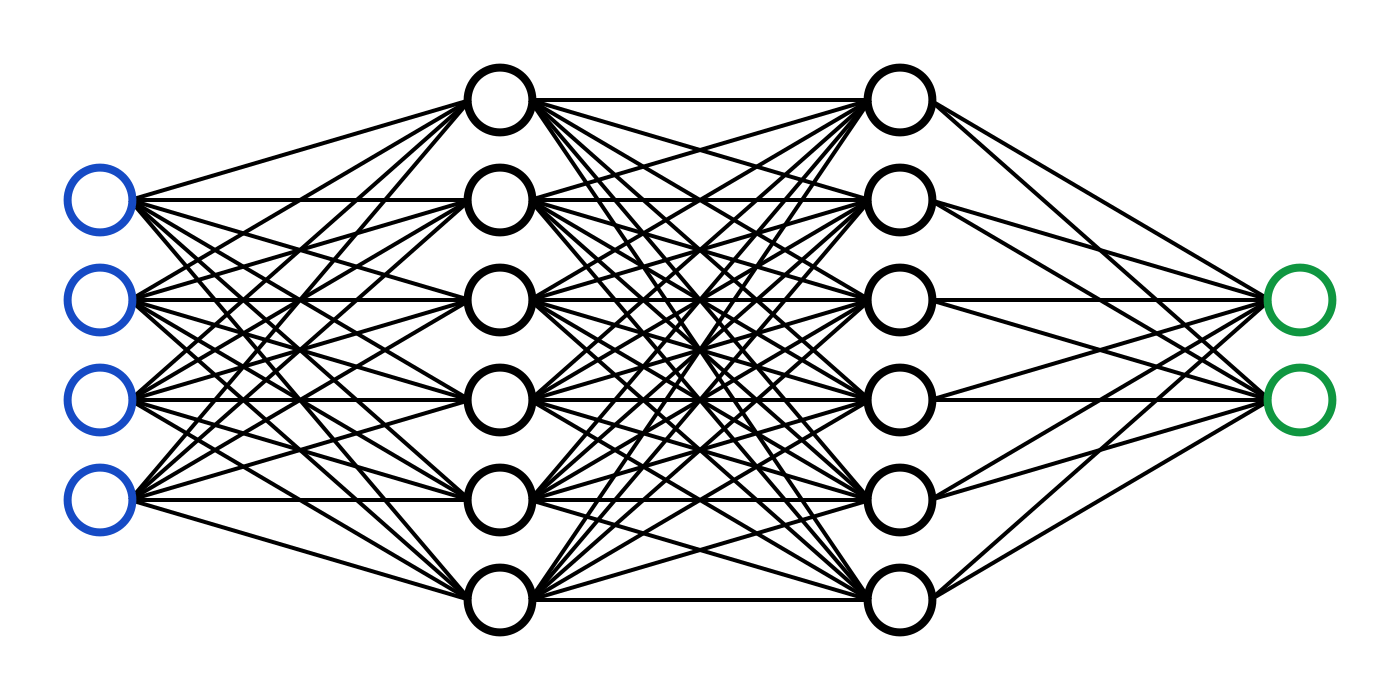
뉴럴 네트워크는 각각이 가중치로 연결되어 신호를 주고받는 간단한 프로세싱 유닛(뉴럴)로 구성되어 있다.
각각의 프로세싱 유닛들이 신호를 주고받는 모습이 마치 사람 뇌의 뉴럴이 상호작용하는 것과 비슷해서 이런 이름이 붙었다.

뉴럴 네트워크는 인풋 레이어, 히든 레이어, 아웃풋 레이어로 나누어볼 수 있다.
예를 들어 y= a*x1+ b*x2+ c일때 입력 x1,x2에 대해 인풋 레이어에 뉴런 2개가 들어가고
출력 y에 대해 아웃풋 레이어에는 1개의 뉴럴이 들어간다.
히든 레이어는 출력 y를 계산하기 위한 여러 겹의 뉴럴들이 존재한다.
Neural Network: 각 뉴럴의 입출력
어떤 하나의 뉴럴 N에서 입력값과 그 입력에 대한 가중치의 곱의 합에 bias를 더한 후 그 값을 Activiation function에 넣어 출력한다.
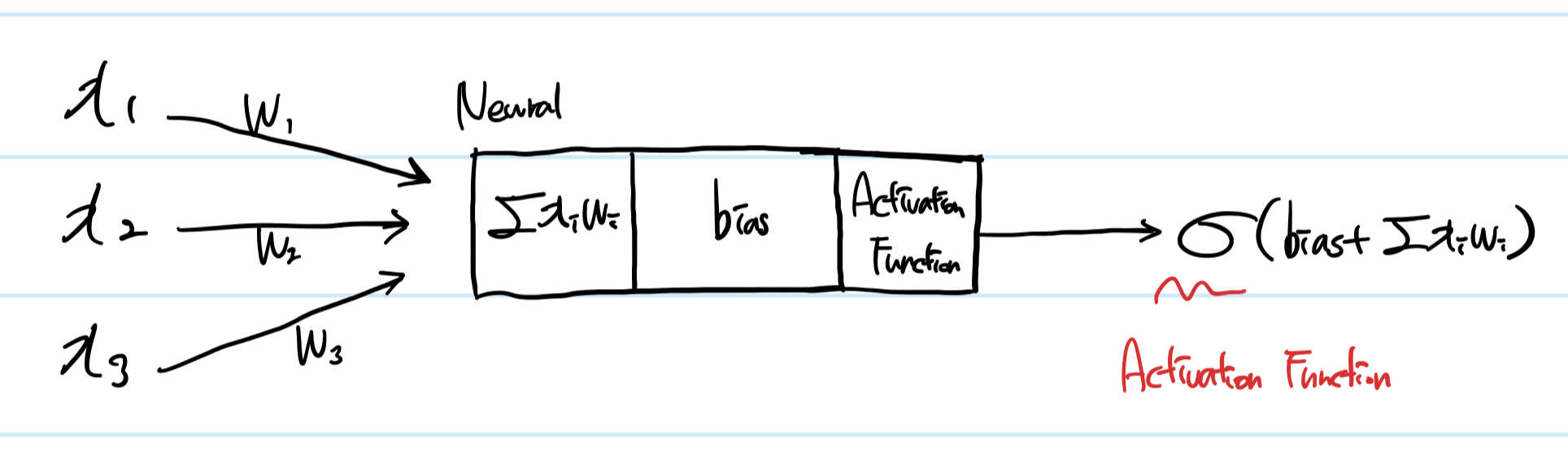
이 계산을 거친 후 출력이 또 입력이 되어 다른 뉴럴에서 이 과정을 반복한다.
Neural Network: Activation Function
활성함수는 추정하려는 값에 따라 선택할 수 있다.
각 뉴런이 계산한 입력값*가중치의 합과 bias를 더한 값을 활성함수에 넣음으로써,
해당 뉴런에서 어떤 방법으로 출력하는지를 결정한다.
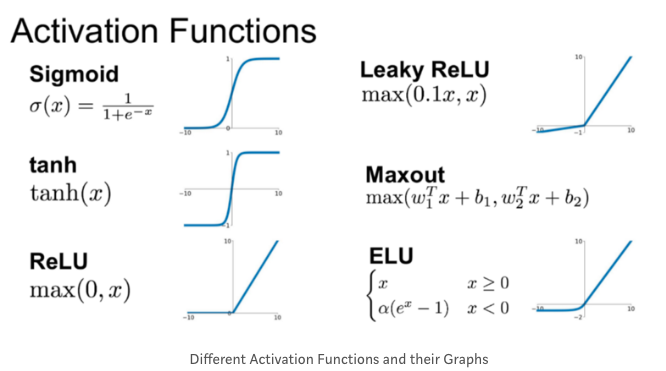
다양한 활성함수가 있지만, sigmoid, tanh, relu에 대해서만 설명하겠다.
Neural Network: Activation Function- Sigmoid
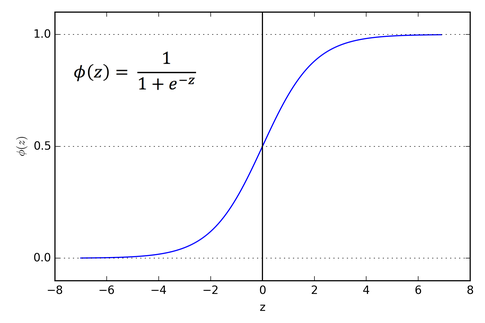
Sigmoid는 0~1사이의 값을 출력한다.
따라서 해당 뉴런이 활성화될 것인지 아닌지를 결정할 때 탁월하지만,
해당 입력의 크기가 크더라도 (0,1)사이로 값이 정의되어 입력의 크기가 출력에 충분히 반영되지 않는다.
(Vanishing Gradient problem; 입력이 1000000000일때와 10일때의 차이가 별로 없다)
게다가 음수는 아예 출력하지 않기 때문에 출력이 음의 방향으로 작용할 수가 없다.
Neural Network: Activation Function- Tanh
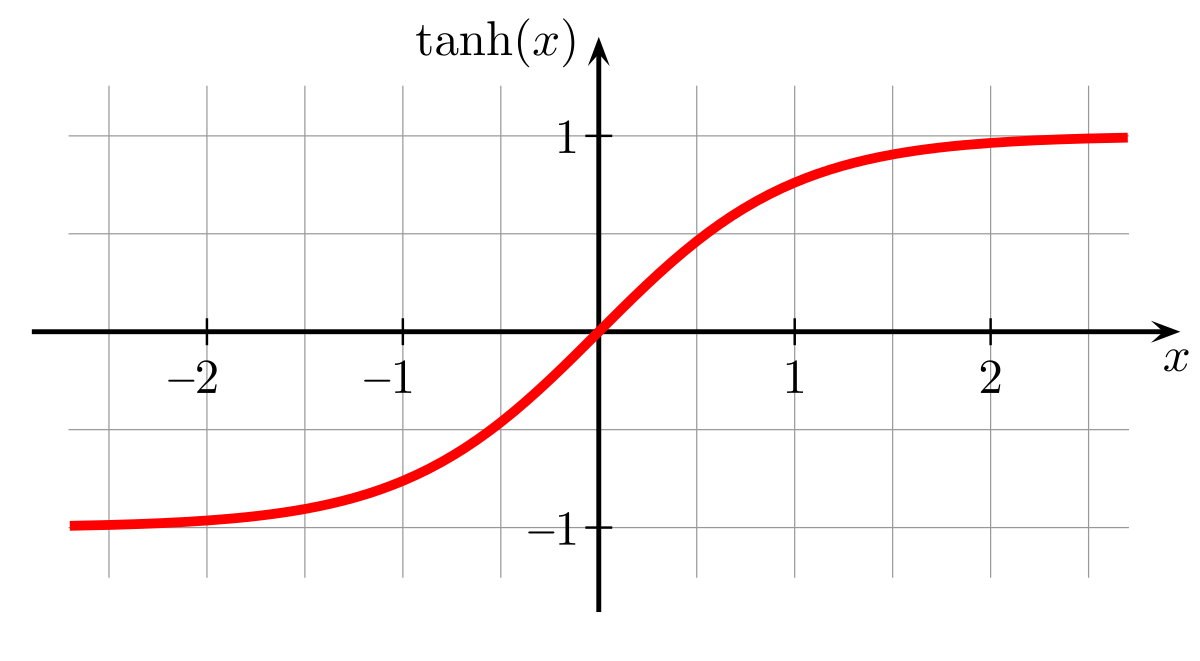
tanh는 sigmoid를 변형한 것으로, (tanh(x)= 2*sigmoid(2x)- 1)
음수를 표현할 수 있고 비교적 더 큰 폭의 범위(-1, 1)를 표현할 수 있다.
그러나 여전히 Vanishing gradient problem은 발생한다.
Neural Network: Activation Function- Relu
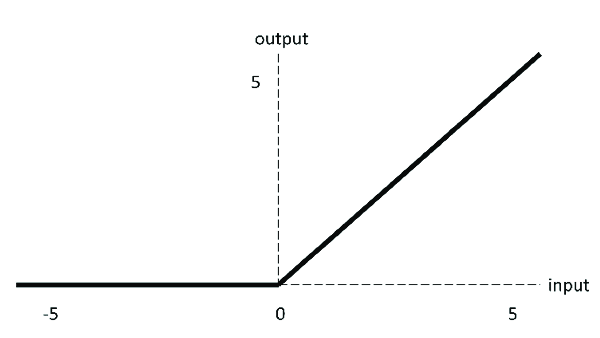
relu는 결과값이 0이상이면 그대로 출력하고, 0보다 작으면 0을 출력하는 함수이다.
따라서 입력의 크기를 출력의 크기에 충분히 반영해줄 수 있어 Vanishing Gradient Problem을 방지할 수 있다.
게다가 판정할 것은 '0 이상이냐 아니냐'가 전부라 속도가 빨라 많이 사용하는 활성함수다.
Neural Network: Hidden Layer

이 뉴럴 네트워크의 히든 레이어의 갯수는 1이다.
히든 레이어는 얼마든지 늘릴 수 있으며 통상적으로는 2~3개 이하의 히든 레이어로 뉴럴 네트워크를 구성한다.
히든 레이어의 갯수가 늘어난다는 것은 무엇을 의미할까?
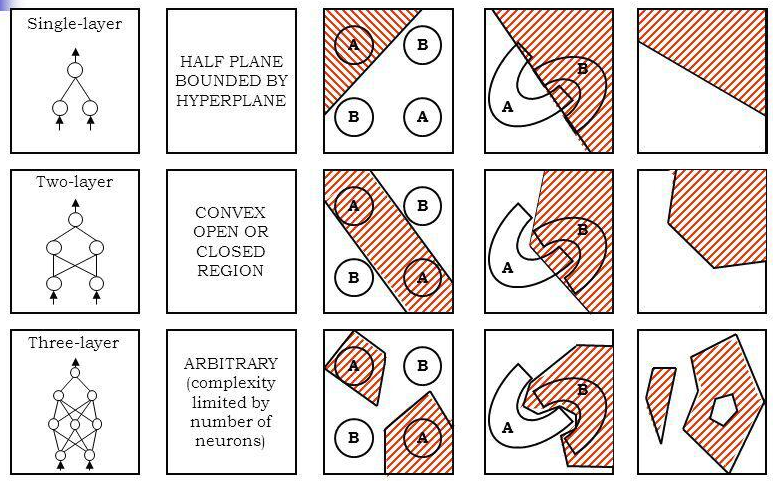
Classification을 예로 들면 레이어의 갯수 증가는 더 복잡한 형태로 분류를 할 수 있게 만든다.
그러나 히든 레이어의 갯수 증가는 곧 전체 네트워크에서 가중치와 뉴럴의 갯수가 늘어난다는 것을 의미하므로,
모델의 학습 속도에 영향을 미친다는 점에 유의해야 한다.
Neural Network: Classification
분류 모델을 만들고자 한다면 뉴럴 네트워크에서 출력 레이어의 갯수가 여러 개가 된다.
입력으로 사진이 주어지고, 이것이 강아지인지 고양이인지 판별할 경우
뉴럴 네트워크의 출력은 강아지-뉴럴 하나, 고양이-뉴럴 하나가 되고,
출력이 가장 큰 뉴럴을 선택해 그것을 결과로 채택한다.
=> 입력-> 출력{강아지=0.4, 고양이=0.6} 이면 그 입력은 고양이로 분류한다.
그것을 위해 분류 모델에서는 출력 레이어에 Softmax를 적용한다.

i번째 output neural 에 대한 값은
softmax= exp_i(z)/Σexp(z)로 정의된다.
여기서 z는 이전 뉴런의 출력이다.
softmax를 적용하면 모든 output neural의 값의 합은 1이 되어 각각으로 분류될 확률이 출력되므로
가장 높은 확률을 가진 뉴럴로 분류되었다고 해석할 수 있다.
학습 데이터의 갯수
학습 데이터의 갯수 N은 가중치의 갯수 |W|와 목표 정확도 a에 대해 다음으로 설정한다.
N> |W|/(1-a)
만약 90%정확도를 보이고 싶다면 가중치의 갯수의 10배만큼의 데이터를 준비해야 한다.
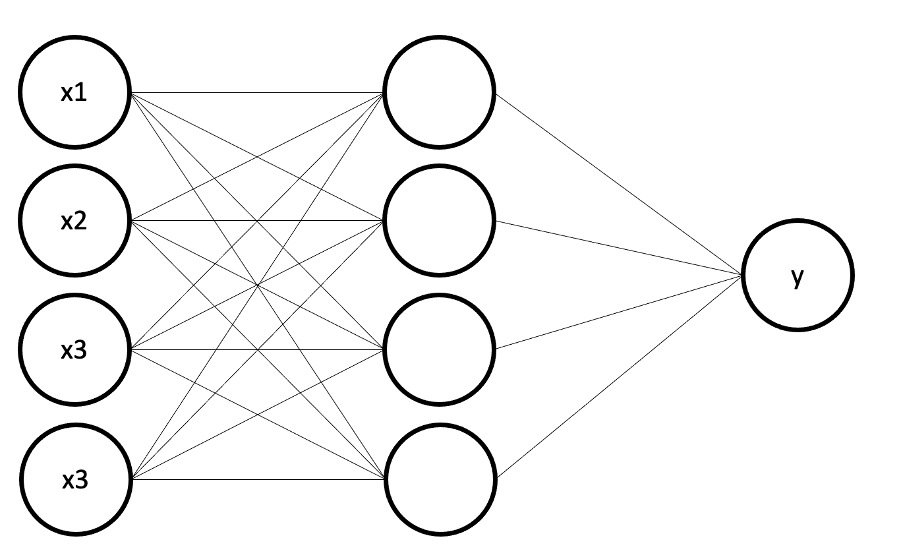
만약 다음과 같은 Full-connected neural network(모든 뉴럴들이 연결되어 있는 상태)에서
가중치는 화살표(연결선)의 갯수이므로, 4*4+ 4= 20개가 되므로
이 때 정확도 90%를 위해서는 학습 데이터는 최소 200개가 되어야만 한다.
Neural Network: Trainning

다시 뉴럴 네트워크의 구성 요소로 돌아와서,
우리가 결정해야 할 요소는 어떤 것들이 있는지 알아보자.
먼저 가중치w의 값을 결정해야 하고,각 뉴럴의 bias를 결정해야만 한다.

그렇다면 이런 뉴럴 네트워크에서 파라미터의 갯수는 몇 개일까?
먼저 가중치의 갯수는 4*4+ 4= 20개이고,
bias의 갯수는 인풋 뉴럴을 제외한 나머지 뉴럴의 갯수와 동일하므로 4+2= 6이 되어
총 26개의 파라미터를 결정해야만 한다.
다른 기법에서와 마찬가지로 NN에서도 Cost Function을 정의하고,
Cost를 최적화하는 파라미터를 선정함으로써 학습할 수 있다.
Neural Network: Gradient Desent & Back propagation을 이용한 학습
Gradient Desent에 대한 간략한 설명은 아래 링크에서 확인할 수 있다.
https://satisfactoryplace.tistory.com/321
[데이터사이언스] Gradient Desent (경사하강법)
Gradient Desent (경사 하강법) 경사 하강법은 cost의 변화량에 따라 파라미터를 움직여가며 cost가 최소가 되는 지점을 찾는 방법이다. J(w)를 cost를 계산하는 함수라고 했을 때, 우리는 J(cost)가 최소가
satisfactoryplace.tistory.com
그렇다면 Back propagation은 무엇일까?

뉴럴 네트워크에서 입력에서 출력 방향으로 계산해나가는 것을 Forward Propagation(앞쪽 방향으로 진행)이라고 한다.
우리는 실제 output과 예측된 output을 알고 있으므로,
Gradient Descent로 가능한 한 오차를 줄이기 위해 parameter를 조정할 수 있음을 안다.
따라서 역방향으로 진행해가며 각 매개변수에 대한 편미분계수를 구해 경사하강법으로
cost의 변화량을 줄여나감으로써 오차를 줄일 수 있으며
이것을 Neural network에서의 trainning 과정이라고 할 수 있겠다.
파이썬 코드로 알아보자
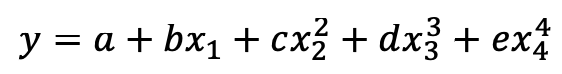
a=1, b=3, c=5, d=10, e= 20으로 결정되었을 때,
y의 산식을 직접 주지 않고 neural network를 이용해 예측할 것이다.

뉴럴 네트워크는 이런 형태가 될 것이다.
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras import initializers
# y= a+ b*x1+ c*x2^2+ d*x3^3+ e*x4^4
def gen_sequential_model(hidden_layer_activation, output_layer_activation, model_optimizer):
model= Sequential([
#input(입력)의 차원은 2
Input(4, name='input_layer'),
#뉴럴의 갯수
#kernel_initializer를 지정해 랜덤으로 weight가 설정되지 않게 할 수 있다
Dense(4, activation=hidden_layer_activation, name='hidden_layer1', kernel_initializer=initializers.RandomNormal(mean=0.0, stddev=0.05, seed= 42)),
# Dense(128, activation=hidden_layer_activation, name='hidden_layer2', kernel_initializer=initializers.RandomNormal(mean=0.0, stddev=0.05, seed= 42)),
Dense(1, activation=output_layer_activation, name='output_layer', kernel_initializer=initializers.RandomNormal(mean=0.0, stddev=0.05, seed= 42))
])
model.summary()
# Stochasitc gradient descent(확률적 경사 하강법) / mean of square error
model.compile(optimizer=model_optimizer, loss='mse')
return model
# 임의의 데이터셋 생성
# 실제: a+ b*x1+ c*x2^2+ d*x3^3+ e*x4^4
def gen_dataset(cnt= 500,a=1,b=3,c=5,d=10,e=20, enable_real_random=False):
if enable_real_random == False:
np.random.seed(0)
#0~1 사이의 4차원 벡터 cnt개만큼 생성
X= np.random.rand(cnt, 4)
X_copy= X.copy()
for vector in X_copy:
vector[1]= vector[1]**2
vector[2]= vector[2]**3
vector[3]= vector[3]**4
coef= np.array([b,c,d,e])
bias= a
#transpose는 행렬을 전치시킴
y= np.matmul(X_copy, coef.transpose())+ bias
return X, y
def plot_loss_curve(history):
import matplotlib.pyplot as plt
plt.figure(figsize=(15, 10))
# plt.gca().set_ylim([0, 1])
plt.plot(history.history['loss'][1:])
plt.plot(history.history['val_loss'][1:])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.show()
def model_fit(model, X, y, epochs=20, verbose=2, validation_split=0.3):
print('enter fitting x: ', X)
print('fitting x: ', X)
history= model.fit(X, y, epochs=epochs, verbose=verbose, validation_split=validation_split)
print('train loss: ', history.history['loss'][-1])
print('test loss: ', history.history['val_loss'][-1])
return history
def predict_new_sample(model, x,a=1,b=3,c=5,d=10,e=20):
x= x.reshape(1,4)
y_pred= model.predict(x)[0][0]
y_actual= a+ b*x[0][0]+ c*(x[0][1]**2)+ d*(x[0][2]**3)+ e*(x[0][3]**4)
# print('\n')
# print('x value= ', x)
# print('y actual value= ', y_actual)
# print('y pred value= ', y_pred)
# print('diff: ', abs(y_actual- y_pred))
return (y_actual- y_pred)
X, y= gen_dataset(cnt=1000)
model= gen_sequential_model('sigmoid', 'relu', 'sgd')
# epochs= 전체 데이터를 몇번 스캔하면서 모델을 만들 것인가
# verbose= 트레이닝 하는 단계에서 loss값을 표현
# validation_split= 테스트(검증)단계에서 사용할 데이터의 비율이 30%
history= model_fit(model, X, y, epochs=300, verbose=2, validation_split=0.3)
def evaluate_model_with_random_dataset():
test_diff= np.array([])
X_test, ___= gen_dataset(cnt=20, enable_real_random=True)
for x in X_test:
diff= predict_new_sample(model, x)
test_diff= np.append(test_diff, np.array([diff]))
test_diff= (test_diff**2)
mse= np.inner(test_diff, np.ones(test_diff.size))/test_diff.size
print('loss of new test dataset(20): ', mse)
evaluate_model_with_random_dataset()
evaluate_model_with_random_dataset()
evaluate_model_with_random_dataset()
plot_loss_curve(history)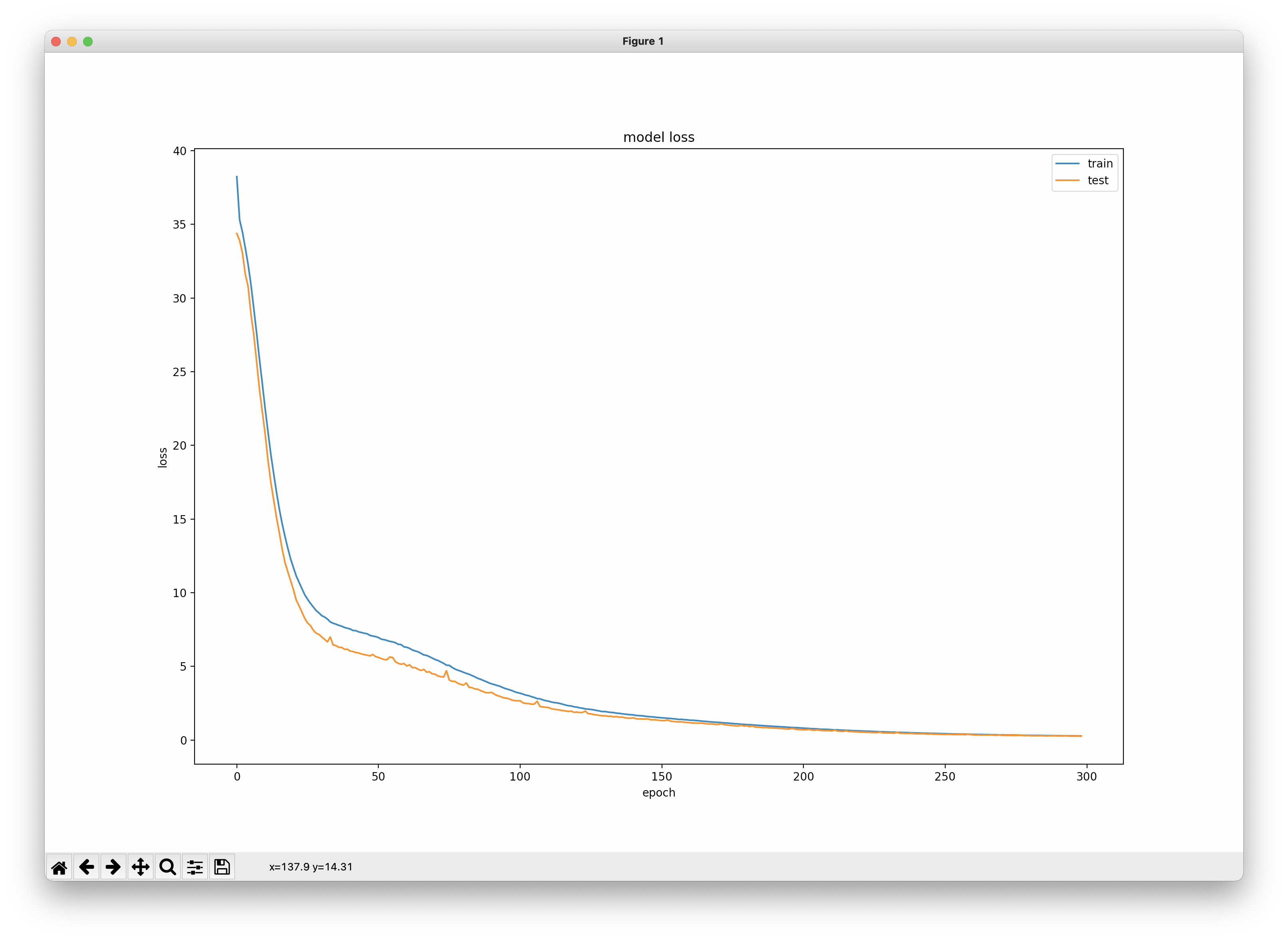
300번의 학습(매 학습마다 back-propagation을 이용해 확률적 경사 하강법으로 loss를 줄임)에 따라
mse(mean of square error)의 값이 어떻게 변화하는지를 시각화한 것이다.

최종적으로 train loss= 0.28, test loss= 0.26이 되었고,
새로운 데이터셋을 생성해 테스트한 결과 0.15~0.17 정도의 평균오차제곱을 보였다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] Convolutioanl Neural Network (CNN) (0) | 2021.12.17 |
|---|---|
| [데이터사이언스] Logistic Regression (0) | 2021.12.17 |
| [데이터사이언스] Gradient Desent (경사하강법) (0) | 2021.12.17 |
| [데이터사이언스] Regression Performance Estimation (회귀 성능 평가) (0) | 2021.10.22 |
| [데이터사이언스] Regression (회귀) (0) | 2021.10.22 |




