만족
[데이터사이언스] Convolutioanl Neural Network (CNN) 본문
[데이터사이언스] Convolutioanl Neural Network (CNN)
데이터사이언스 Satisfaction 2021. 12. 17. 19:33Image Classification 등 입력의 갯수가 많을 때 Full-connected Neural Network를 사용하면
조정해야 할 파라미터의 갯수가 너무 많아 학습시간이 너무 오래 걸린다.
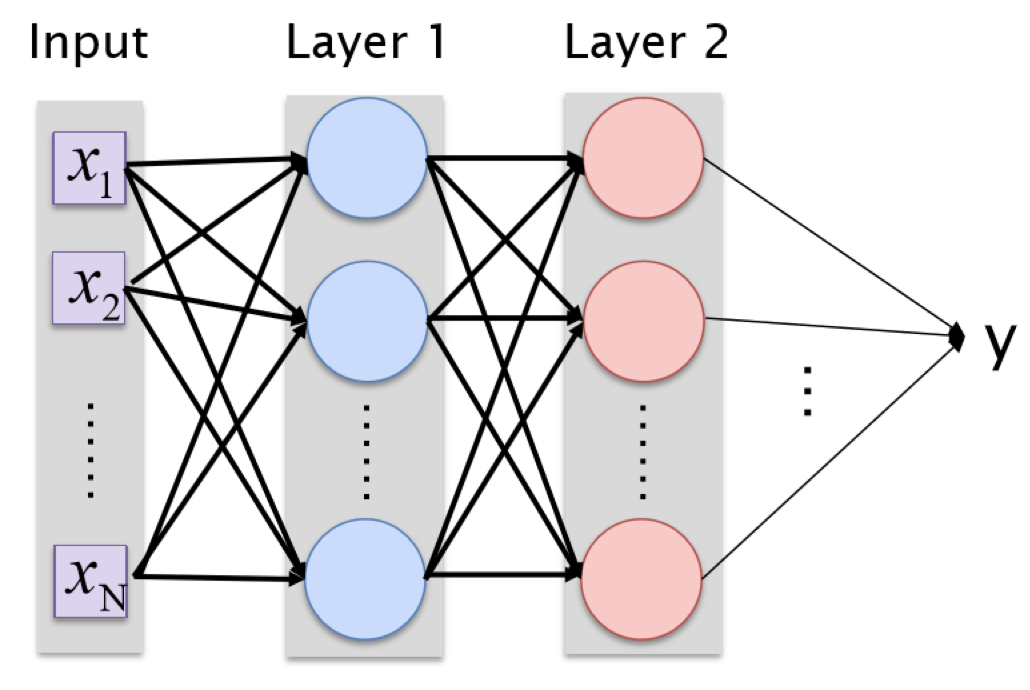
크기가 64*64 해상도인 사진 입력과 히든 레이어 2겹, 각 1000개의 뉴런에 대해 y를 계산하려면
64*64*1000+ 1000*1000+ 1000개의 파라미터에 대해 최적화를 진행해야 한다.
이것은 학습 시간이 오래 걸린다는 것을 의미하기도 하지만,
너무 많은 학습 데이터를 요구한다는 것을 의미하기도 한다.
(학습 데이터의 갯수는 가중치를 원하는 정확도로 나눈 값이 최소값으로 하는 것이 권장된다)
Convolutional Neural Network
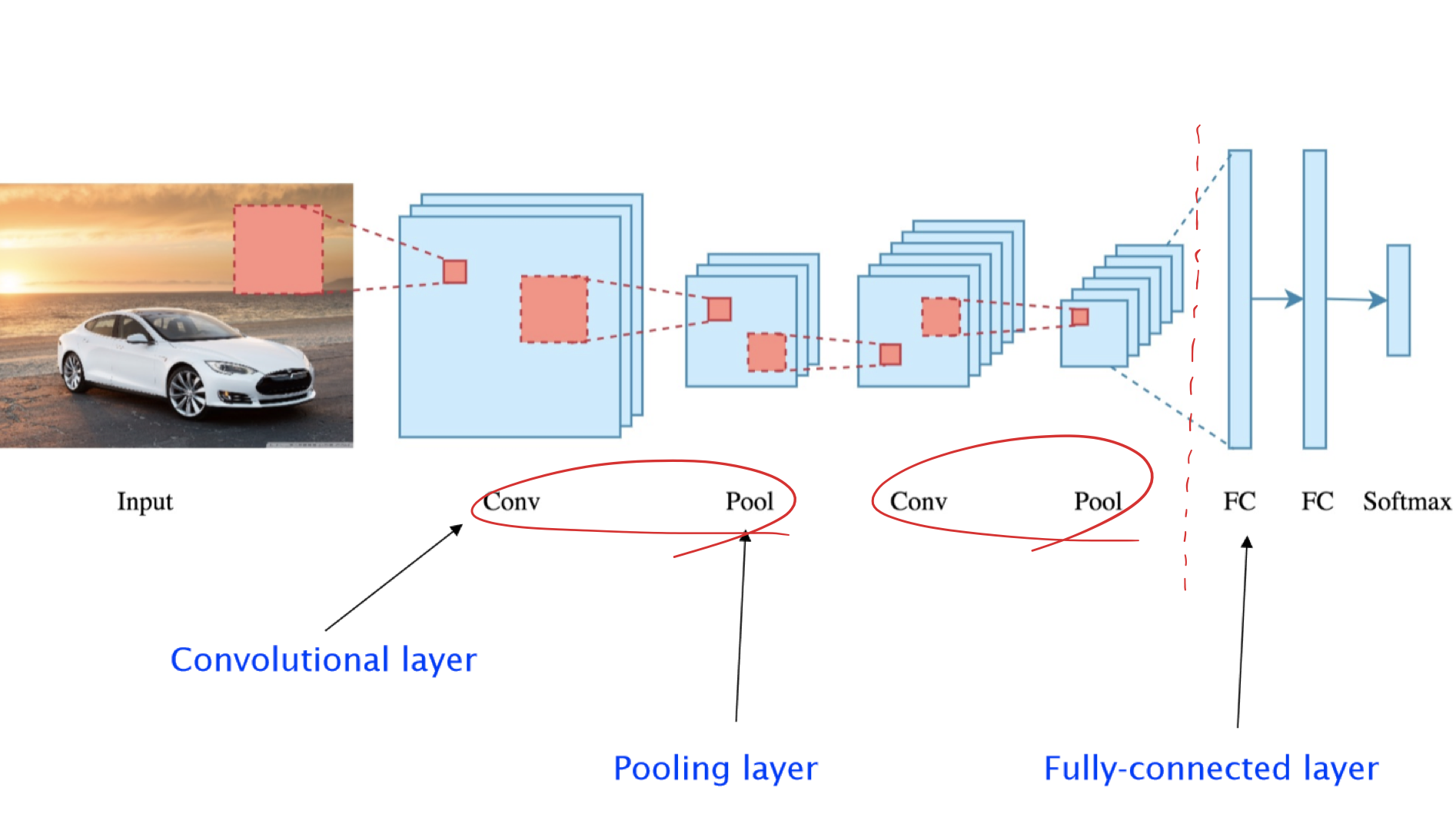
바로 Neural Network를 사용하지 않고, N겹의 Convolutional/Pooling layer를 사용해 입력을 줄이고,
이후 Full-connected layer를 사용해 softmax로 분류를 마친다.
Convolutional/Pooling layer는 각 데이터의 특징을 뽑아 더 작은 출력으로 변환하는 역할을 한다.
따라서 즉시 Full-Connected layer를 사용할 때 보다 더 적은 학습 데이터와 학습 시간을 요구하게 된다.
Convolution
Convolution은 입력과 filter에 대해 연산하여 입력의 크기를 줄여서 출력한다.
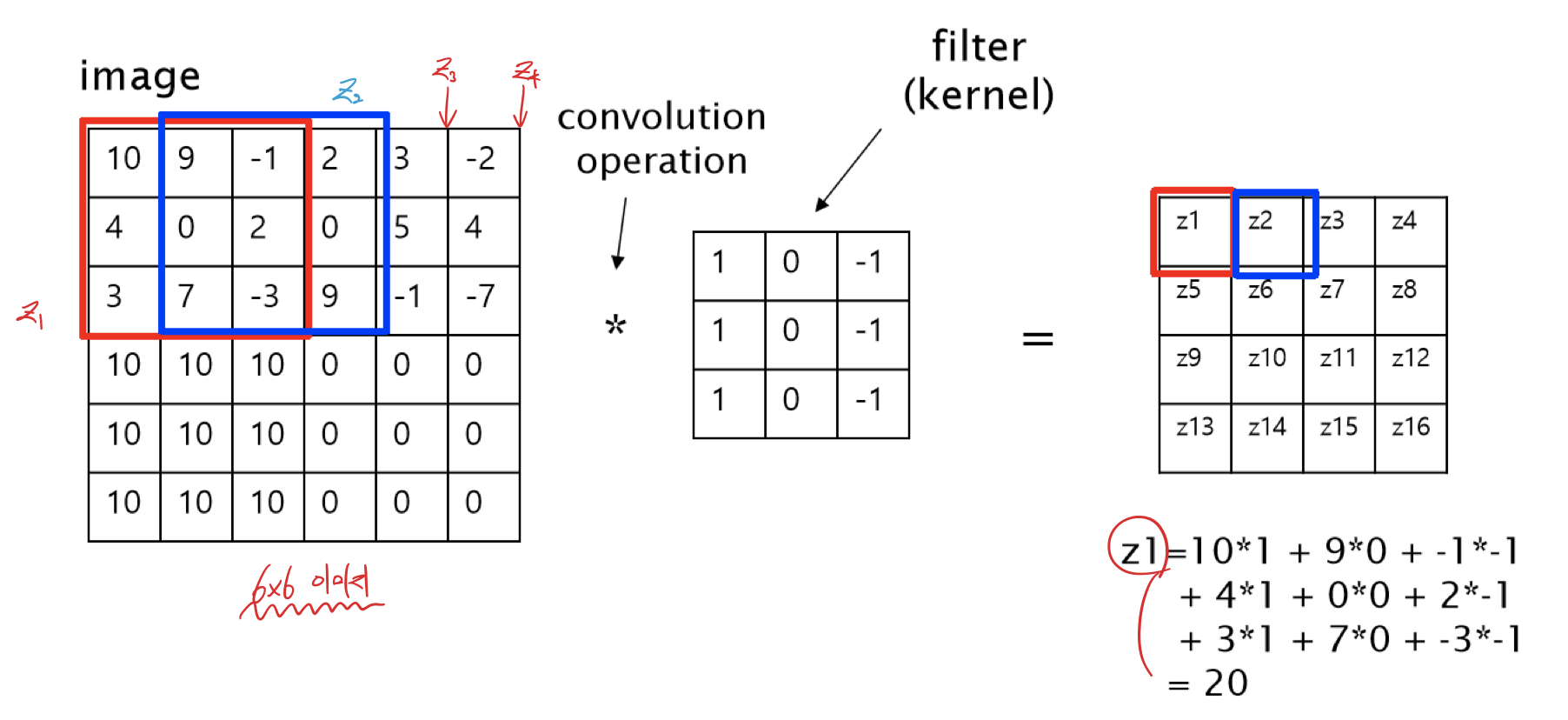
출력 z1~z16을 계산하기 위해서 image의 filter크기만큼의 영역을 잘라 filter의 각 원소와의 곱의 합을 zi에 할당한다.
z1의 경우 image의 붉은 영역과 filter의 각 원소의 곱의 합이 z1값이 된다.
이것을 z16까지 반복함으로써 Convolution 연산의 결과를 얻을 수 있다.
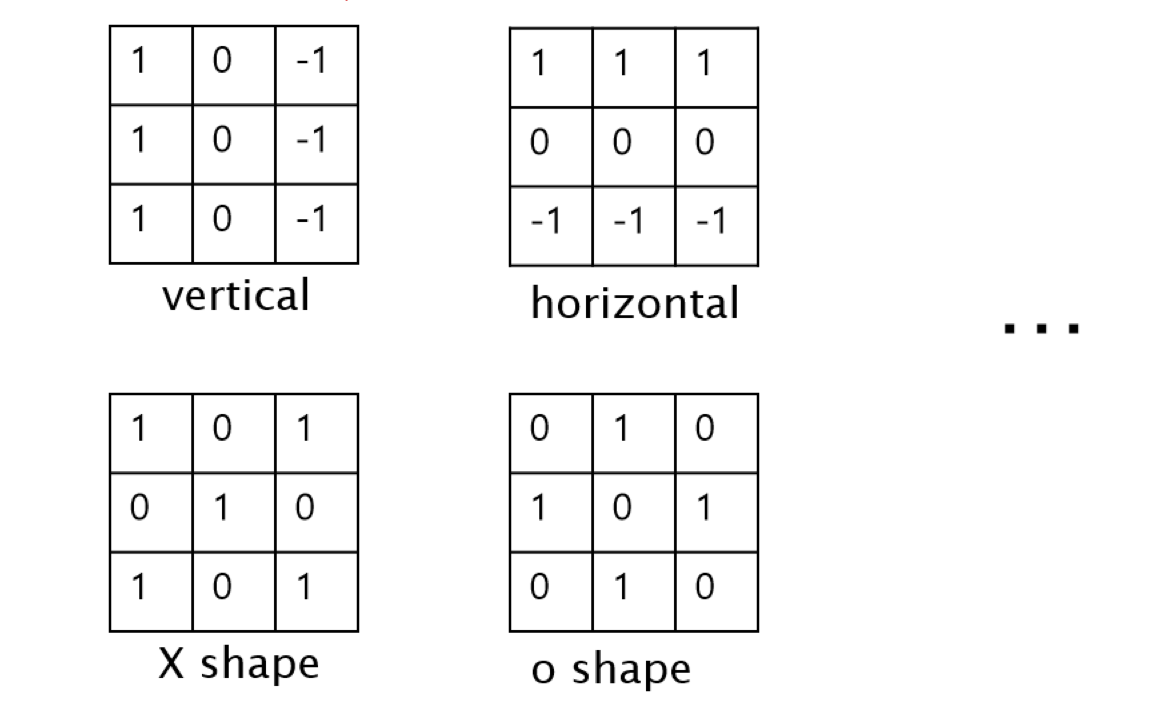
filter는 용도에 따라 다른 값을 사용한다.
위의 필터는 수직선 필터이며, 다양한 필터들이 존재한다.
만약 입력이 여러 채널(흑백이미지가 아닌 RGB이미지)인 경우는 어떻게 할까?
RGB의 경우 3개의 채널로 이루어져 있으므로 이미지를 각 채널로 분해하고,
그 채널에 대해 각각 Convolution 연산을 시행한다.
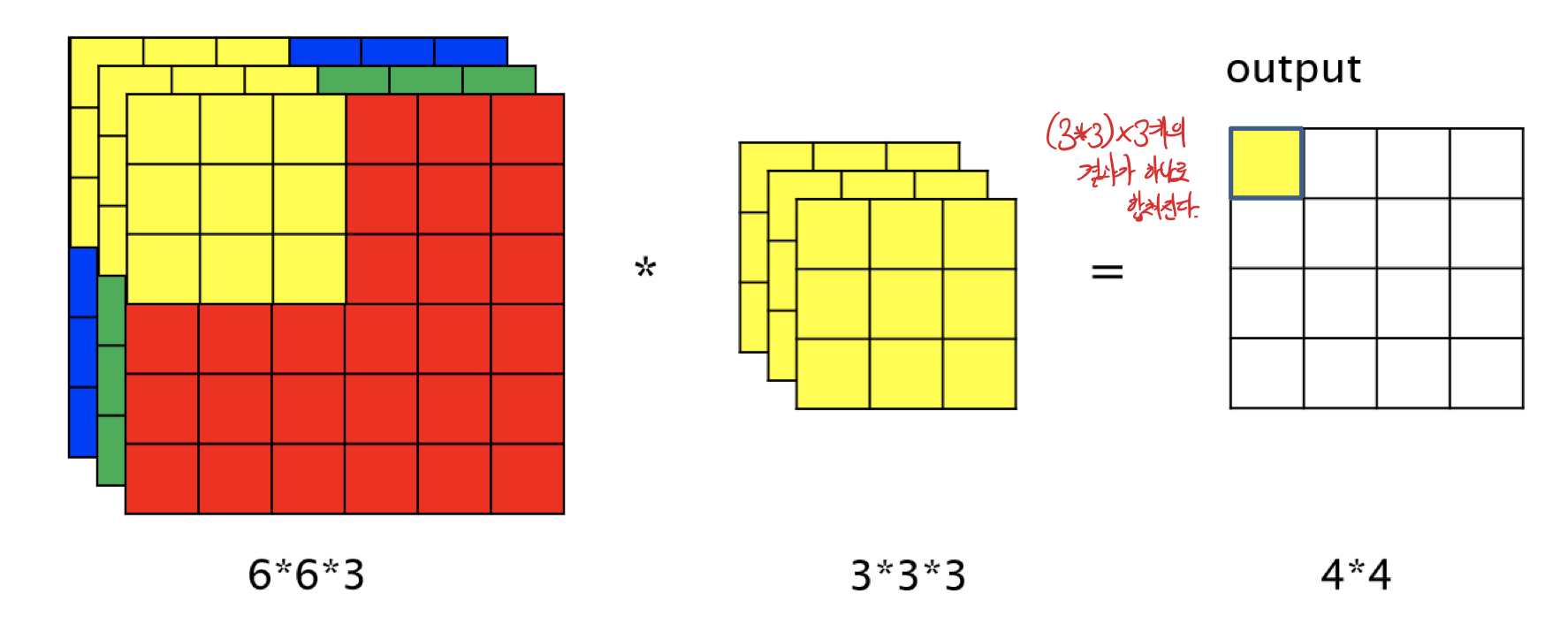
각각의 채널에 대해 구한 z값들을 병합하여 출력은 1채널이 된다.
그렇다면 만약 여러 종류의 필터를 사용하면 어떻게 될까?
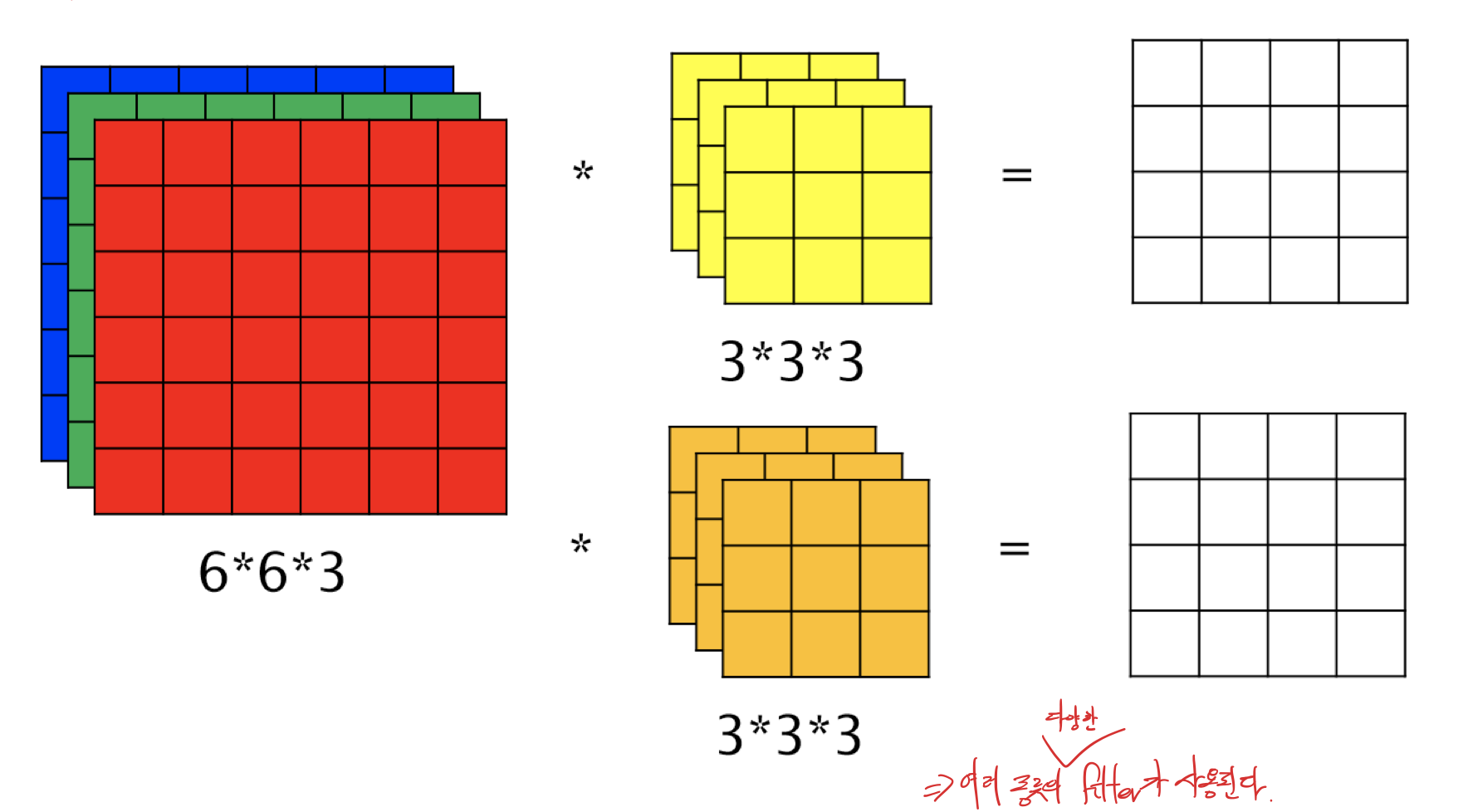
여러 종류의 filter가 사용되면 결과값 역시 그 filter의 갯수만큼 늘어난다.
여기에서 우리가 최적화하고자 하는 것은 filter의 형태이다.
따라서 filter의 각 원소를 f1, f2 ... 라고 하면 이 f들이 parameter가 된다.
이 값을 최적화하기 위해 gradient desent 등 우리가 알고 있는 최적화 방법들을 사용할 수 있다.
Pooling
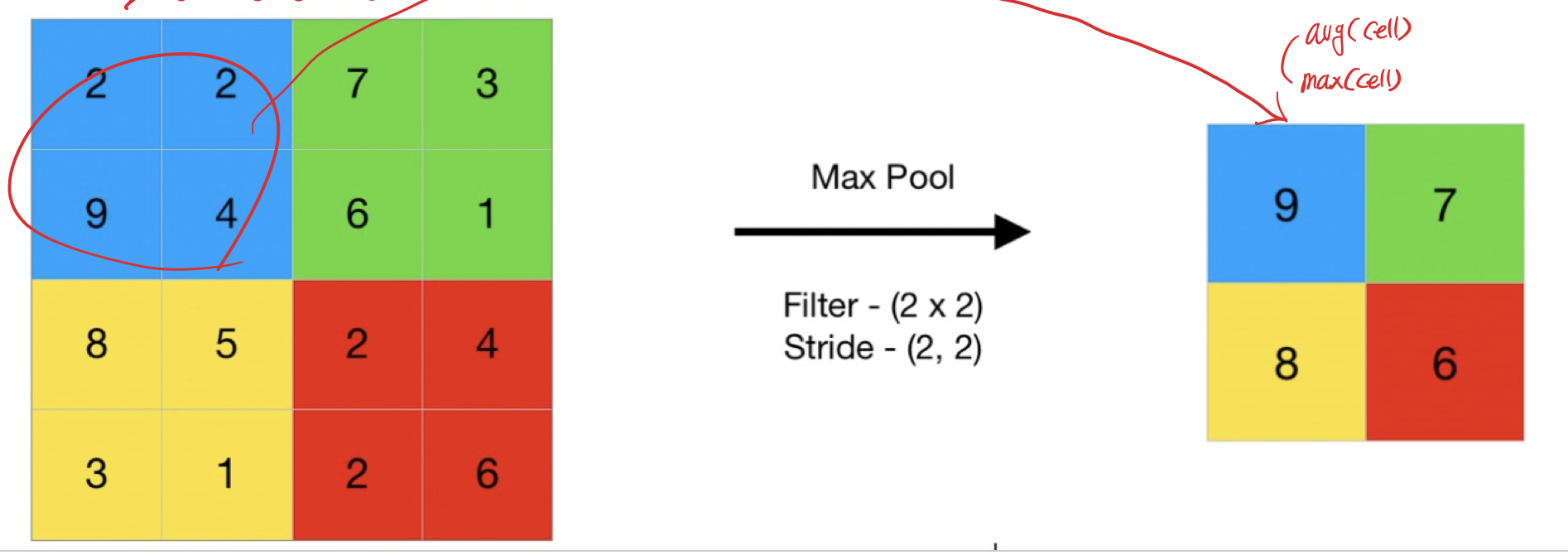
Pooling Layer에서는 단순히 입력의 크기를 줄여 출력하는 역할을 한다.
입력의 특정 영역에서 max, avg 등의 방법으로 그 영역의 대표성을 띄는 원소값으로 축소하여 출력한다.
이 레이어에서 trainning paramter는 존재하지 않는다.
파이썬으로 알아보자
mnist 데이터셋을 이용해 필기체 이미지를 모델에 학습시켜,
필기체 이미지가 입력으로 주어지면 그것이 어떤 숫자인지를 예측할 것이다.
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import Input, Conv2D, MaxPooling2D, Dense, Flatten
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.datasets import mnist
def plot_loss_curve(history):
import matplotlib.pyplot as plt
plt.figure(figsize=(15, 10))
# plt.gca().set_ylim([0, 1])
plt.plot(history.history['loss'][1:])
plt.plot(history.history['val_loss'][1:])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.show()
def train_mnist_model():
(X_train, y_train), (X_test, y_test)= mnist.load_data();
# plt.imshow(X_train[0], cmap='gray')
# plt.show()
# channel이 한개라는 것을 명시
X_train= X_train.reshape(60000, 28, 28, 1)
X_test= X_test.reshape(10000, 28, 28, 1)
# print(X_train.shape);
# print(y_train);
# to_categorical은 결과를 one-hot encoding으로 표현법 변경
# ex) result:0 => 1,0,0,0,0,0,0,0,0
# ex) result:1 => 0,1,0,0,0,0,0,0,0
# ...
y_train= to_categorical(y_train)
y_test= to_categorical(y_test)
model= Sequential([
Input(shape=(28,28,1), name='input_layer'),
# kernel_size는 conv에서 사용할 filter의 크기를 말한다
# 3이면 3*3 크기의 행렬 생성
# 32는 커널의 갯수 (kernel_cnt)
# param의 갯수가 320인 이유
# filter_size= 3*3이므로
# 뉴런갯수 32에 filter_size+1을 곱하여 320이 된다.
Conv2D(32, kernel_size=3, activation='relu', name='conv_layer1'),
# Dropout(0.5)
MaxPooling2D(pool_size=2),
# 뉴런에 사용할 데이터셋은 1차원 벡터만 가능한데 Pooling 시에는 그렇지 않기 때문에
# 평면화가 필요하다
Flatten(),
Dense(10, activation='softmax', name='output_layer')
])
model.summary()
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history= model.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=10, epochs=3)
print('train loss: ', history.history['loss'][-1])
print('test loss: ', history.history['val_loss'][-1])
plot_loss_curve(history)
model.save('mnist.model')
return model
def predict_image_sample(model, X_test, y_test, test_id=-1):
if test_id< 0:
from random import randrange
test_sample_id= randrange(10000)
else:
test_sample_id= test_id
y_actual= y_test[test_sample_id]
print('y_actual= ', y_actual)
test_image= X_test[test_sample_id].reshape(1,28,28,1)
y_pred= model.predict(test_image)
print('y_pred= ', y_pred)
y_pred= np.argmax(y_pred, axis=1)[0]
print('y_pred number= ', y_pred)
(X_train, y_train), (X_test, y_test)= mnist.load_data();
model= train_mnist_model()
predict_image_sample(model, X_test, y_test)출력값
y_actual= 1
y_pred= [[1.1533230e-08, 9.9995887e-01, 5.6455626e-08, 1.5423840e-08, 2.7865196e-06, 5.1418045e-08, 3.2636951e-08, 3.5088348e-08, 3.8287413e-05, 2.0787017e-08]]
y_pred number= 1
출력에서 y_pred는 output layer의 값들을 말한다.
분류 모델이므로 이 중에서 가장 큰 값이 예측값이 된다.
이 케이스에서는 1번 인덱스의 값(9.9995887e-01)이 가장 높은 값이였으므로, 1로 예측하였다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] Neural Network (뉴럴 네트워크) (0) | 2021.12.17 |
|---|---|
| [데이터사이언스] Logistic Regression (0) | 2021.12.17 |
| [데이터사이언스] Gradient Desent (경사하강법) (0) | 2021.12.17 |
| [데이터사이언스] Regression Performance Estimation (회귀 성능 평가) (0) | 2021.10.22 |
| [데이터사이언스] Regression (회귀) (0) | 2021.10.22 |




