만족
[데이터사이언스] 데이터 요약과 시각화 (Data summary and visualization) 본문
[데이터사이언스] 데이터 요약과 시각화 (Data summary and visualization)
데이터사이언스 Satisfaction 2021. 10. 21. 19:19Summary Statistics
데이터의 속성을 나타내는 숫자값이다.
(평균, 표준편차 분산 등)
Summary Statistics: Mean(평균)
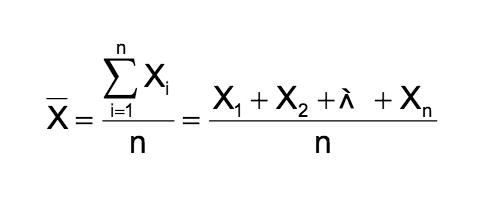
데이터 값들의 합을 데이터 갯수로 나눈 값이다.
가장 흔하게 사용되지만 이상값에 민감하게 반응({0,0,0,1000}의 평균값은 250이다)하여
median(중간값), trimmed mean(이상값을 제외한 평균값)과 함께 사용된다.
Summary Statistics: Median(중앙값)

정렬된 데이터셋의 중앙에 위치하는 값이다.
데이터의 갯수가 짝수개일 때는 중앙에 있는 값들을 더한 후 2로 나눈 값을 중앙값으로 사용한다.
Symmetric Data vs Skewed Data

중앙값(Median), 최빈값(Mode), 평균값(Mean)이 모여있으면 Symmetric,
그렇지 않고 한쪽으로 치우쳐져 있으면 Skewed 라고 한다.
Summary Statistics: Variance(분산)
V= Sigma( (E-X)^2 ) / N
=> E: 평균, X: 데이터값, N: 데이터 갯수
평균에서 데이터 값들을 뺀 값을 제곱하여 모두 더한 값을 N으로 나눈 값을 분산이라 한다.
(E-X를 제곱한 것은 음수가 나오지 않게 하기 위해서이다)
분산은 데이터들이 평균에서 얼마나 떨어져 있는지를 대표하는 값이다.
Summary Statistics: Variance(분산)값 보정
Variance값은 이상값에 영향을 크게 받는다.
따라서 이런 현상을 가능한 줄이기 위해 다른 지표들을 사용할 수도 있다.
AAD(Average of Absolute Deviation)
AAD= Sigma( |E-X| ) / N
=> 평균과 데이터값의 차를 제곱하는 대신 절대값으로 계산한다.
MAD(Median of Absolute Deviation)
MAD= median( |E-x0|, |E-x1|, .... |E- xn| )
Interquartile Range
interquartileRange= x(75%) - x(25%)
=> 데이터셋 x의 퍼센타일 75%값(하위 75%에 위치하는 값)에서 퍼센타일 25%값(하위25%에 위치하는 값)을 뺀 값이다.

=> Interquartile Range값이 크다는 것은 데이터가 25%~75% 사이에 밀집되어 있다는 것을 의미한다.
Summary Statistics: Standard deviation(표준편차)
분산의 양의 제곱근을 말한다.
분산을 구할 떄 (E-X)^2를 했기 때문에 분산값은 과대계상될 수 있기 때문에,
분산에 루트를 씌워 다시 보정한 값이다.
Summary Statistics: Percentile
데이터셋에서 주어진 백분위 위치에 존재하는 데이터의 값을 말한다.
Percentile(25)는 데이터셋에서 하위 25% 위치에 존재하는 데이터값을 말한다.
(ex: {1,2,3,4}에서 P(0)= 1)
Summary Statistics: Five Number Summary
5개의 일정한 간격의 백분위수에 위치하는 Percentile value를 말한다.
0%(min), 25%, 50%(median), 75%, 100%(max) 위치를 사용하고
각각 Q1, Q2 ... Q5로 약식표기한다.
Visualization: Boxplot

Boxplot으로 데이터를 표현할 때 Five Number Summary 값들을 사용한다.
박스부분은 25%~ 75%가 포함된다.
점선부분은 이상값들을 제외한 백분위 25%이하의 데이터 값들과 75%이상의 데이터 값을 표시한다.
점선부분을 넘어 o 모양으로 찍힌 값들은 이상값(outlier)이며, 계산방법은 다음과 같다.
Lower Extreme;하위 이상값 기준치: X(25%)- 1.5* IRQ 보다 작으면 이상값
Upper Extreme;상위 이상값 기준치: X(75%)+ 1.5* IRQ 보다 크면 이상값
IRQ(interquarile range)= X(75%)- X(25%)
Visualization: Histogram

각 데이터 값 구간에 대한 빈도수(Frequency)를 나타낸 다이어그램이다.
Histogram에서는 데이터의 분포 형태를 알 수 있으며,
다른 형태의 Histogram이라도 Boxplot에서는 동일하게 나타날 수 있다.
(Boxplot은 분산을 고려하지 않고 Q1~Q5과 관련된 값들을 표현하기 때문이다)
Visualization: Scatter plot

2개 이상의 변수간의 관계를 시각화해주는 다이어그램이다.
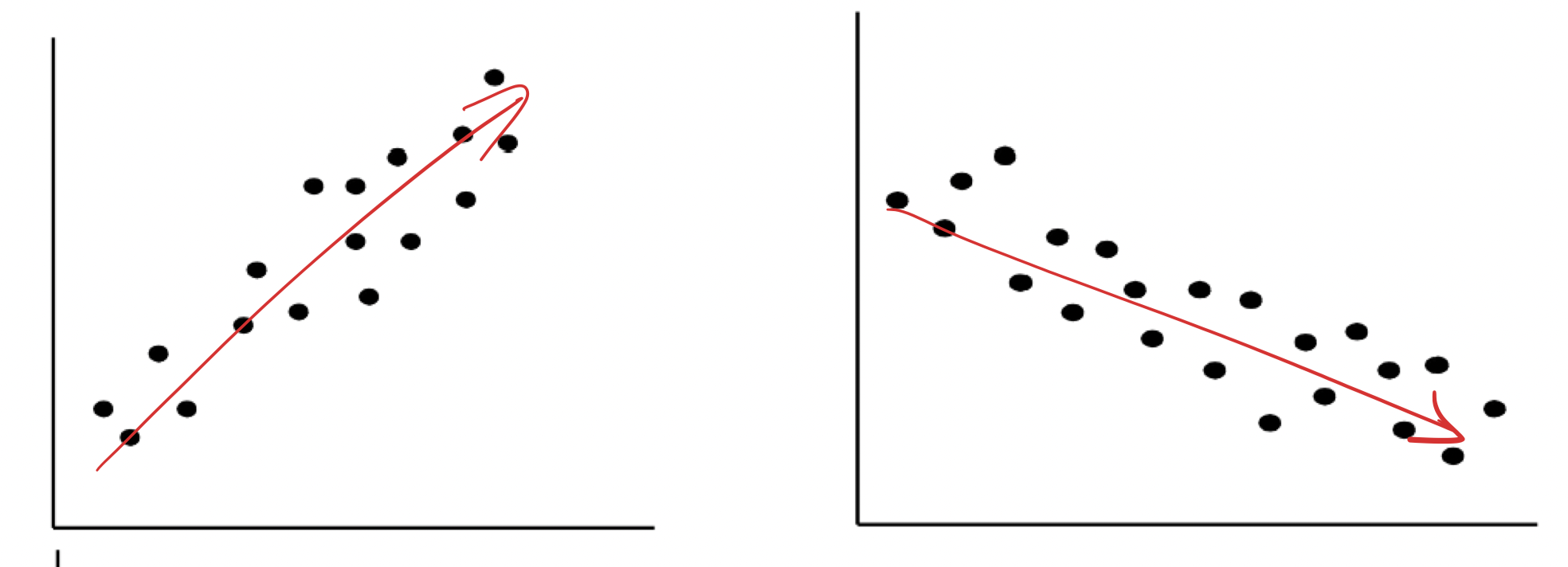
연관이 있는 변수의 경우 다음처럼 특정 모양으로 밀집되는 경향이 있다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] 머신러닝 개요 (0) | 2021.10.22 |
|---|---|
| [데이터사이언스] 유사도(Similarity) (0) | 2021.10.22 |
| [데이터사이언스] 공분산(Covariance)과 상관관계(Correlation) (0) | 2021.10.21 |
| [데이터사이언스] 데이터의 이해 (0) | 2021.10.20 |
| [데이터사이언스] Numpy, Pandas, Dataframe (0) | 2021.10.20 |


