만족
[데이터사이언스] 공분산(Covariance)과 상관관계(Correlation) 본문
[데이터사이언스] 공분산(Covariance)과 상관관계(Correlation)
데이터사이언스 Satisfaction 2021. 10. 21. 20:12Covariance(공분산)
공분산은 두 변수가 변화할 때 어떤 연관성이 있는지를 나타내는 척도이다.
=> 한 변수가 변했을 때 다른 변수의 변화량에 얼마나 영향을 주는가?
(ex: BMI지수와 성인병의 발병률은 어떤 연관성이 있는가?)
분산V= Sigma( (X-E)^2 ) / N= E((X- E(X))^2)
공분산Cov= E( (X-E(X) * (Y-E(Y)) )
공분산은 각 변수가 각 평균에서 떨어진 만큼의 거리의 평균을 의미한다.
공분산 값(양수/음수)에 따라 어떤 연관성이 있는지를 알아낼 수 있다.
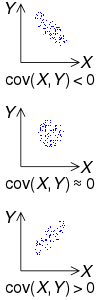
위와 같이 cov가 양수이면 X가 증가할 때 Y도 증가하고,
cov가 음수이면 X가 증가할 때 Y는 감소하는 양상을 띈다.
그러나 cov의 절대값이 큰 것이 연관관계가 크다는 것을 의미하지는 않는다는 것에 주의하자.
(분산이 큰 변수끼리는 연관성에 관계없이 공분산도 크게 나올 수 있다)
Correlation(상관관계)
공분산이 "연관성이 존재하는가?"에 초점을 맞추었다면
상관관계는 "그럼 얼마나 연관성이 있는가?"에 초점을 맞춘다.
Cov(xy)= E( (X-E(X)) * (Y- E(Y)) )
Correlation(xy)= r= Cov(xy)/(S(x)*S(y))
S(x)는 x의 표준편차(Standard deviation)
S(y)는 y의 표준편차
상관관계는 강도(r)로 나타나고, 공분산을 각 변수의 표준편차의 곱으로 나눈 값으로 구할 수 있다.
강도(r)은 [-1, 1] 사이값으로 나타난다.
그 이유는 아래와 같다.
//자기자신간의 공분산은 정의에 의거해 표준편차의 제곱과 같다
Cov(xx)= S(x)* S(x)
//따라서 아래가 성립한다
Cov(xx)/(S(x)*S(x))= 1
Cov(xy)<= S(x)* S(y) // 공분산과 표준편차 정의에 따라서
-1<=Cov(xy)/(S(x)* S(y))<= 1 //공분산은 음수일 수도 있으므로
다시 상관관계를 구하는 식으로 돌아가서, Z 스코어 표준화를 진행하면 아래와 같다.
Z표준화 시, Z= (X- M)/S= (변수- 평균)/표준편차
이므로
r= Cov(x,y)/(S(x)*S(y))= Sigma(z(x)*z(y))/ N
로도 표현할 수 있다
r= Sigma(z(x)* z(y))/N 으로 나타낸 것을 Pearson correlation coefficient(피어슨 상관 계수)라고 한다.
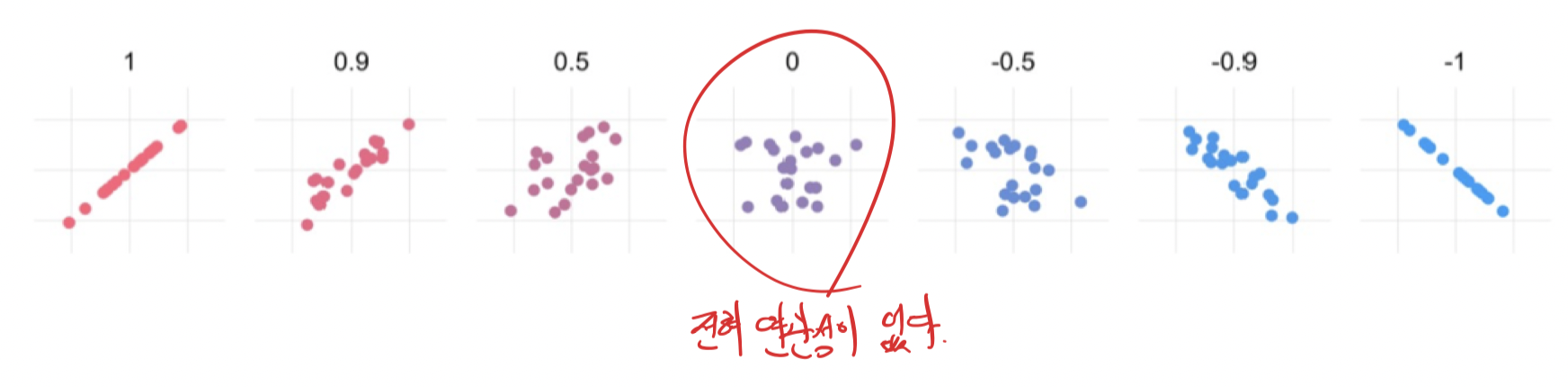
이 상관 계수를 통해 데이터의 변화 형태를 유추할 수 있다.
Covariable과는 달리 Correlation을 통해 얼마나 연관 강도가 있는지를 알아낼 수 있기 때문이다.
(if r<0, x가 증가할 때 y는 감소)
(if r>0, x가 증가할 때 y도 증가)
Covariance(공분산) vs Correlation(상관관계)
Covariance: 두 변수의 선형 관계의 방향을 알려준다.
Covariance: 두 변수의 선형 관계의 방향과 강도까지 알려준다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] 머신러닝 개요 (0) | 2021.10.22 |
|---|---|
| [데이터사이언스] 유사도(Similarity) (0) | 2021.10.22 |
| [데이터사이언스] 데이터 요약과 시각화 (Data summary and visualization) (0) | 2021.10.21 |
| [데이터사이언스] 데이터의 이해 (0) | 2021.10.20 |
| [데이터사이언스] Numpy, Pandas, Dataframe (0) | 2021.10.20 |



