만족
[데이터사이언스] 유사도(Similarity) 본문
[데이터사이언스] 유사도(Similarity)
데이터사이언스 Satisfaction 2021. 10. 22. 08:12Similarity(유사도)
두 데이터가 얼마나 유사한지를 수치적으로 나타낸다.
[0,1] 사이의 값으로 나타나며, 두 데이터가 높을수록 1에 가까운 수로 표현된다.
Dissimilarity(비유사도)
두 데이터가 얼마나 다른지를 수치적으로 나타낸다
0이상의 값으로 나타나며 완전히 같을 경우 0으로 표현된다.
(상한값은 데이터에 따라 다르다)
Similarity vs Dissimilarity: Data type
데이터 타입에 따라 유사도와 비유사도를 표현하는 방법이 다르다.
p, q를 각 데이터의 attribute라고 하자.
| Dissimilarity | Similarity | |
| Nominal (순서가 없는 데이터; 직업) | 같으면 0, 다르면 1 | 같으면 1, 다르면 0 |
| Ordinal (순서가 있는 데이터; 옷 사이즈) | 각 데이터를 0부터 n-1까지 매핑하고 |p-q|/(n-1)로 계산한다 |
1- dissimilarity값으로 계산한다. 1- (|p-q|/(n-1)) |
| Interval or Ratio (수치 데이터; 몸무게) | |p-q| | 세 가지 방식으로 정의된다. 1) -|p-q|= -dissimilarity 2) 1/(1+ |p-q|)= 1/(1+ dissimilarity) 3) 1- (d- min(d))/(max(d)- min(d)) (단 d는 dissimilarity) |
이처럼 데이터 타입에 따라 유사도와 비유사도를 구하는 방법이 다르다는 것을 알 수 있다.
Minkowski Distance(민콥스키 거리) in Vector
민콥스키 거리는 유클리드 거리의 일반화이다.
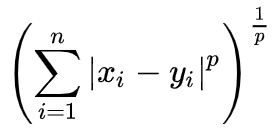
민콥스키 거리는 다음과 같이 구할 수 있으며,
n은 차원(attribute 갯수), p는 파라미터를 의미한다.
p=1일땐 맨하탄 거리,
p=2일땐 유클리드 거리(2차원공간에서 점과 점사이의 거리)
p=infinite일땐 수프리멈 거리(n차원공간 중에서 가장 큰 축의 길이; max(|xi-yi|))가 된다.

x1(1,1), x2(2,2) 에 대해 p=1,2,..infinite 값을 구해보면 위와 같이 몬콥스키 거리를 구할 수 있다.
p가 작을수록 distance값이 커지고, p가 클수록 각 축의 최대길이에 가까워짐을 확인할 수 있다.
Dissimilarity about distance
위 거리값을 이용해 비유사도 계산도 사용할 수 있다.
distance(p,q)는 p와 q의 거리를 의미하므로,
유사하지 않다면(멀리 떨어져 있다면) 거리값은 크게 나타나고
유사하다면 거리값은 작게 나타날 것이다.
(distance(p,q)= dissimilarity(p,q); d(p,q)로 표현)
Dissimilarity(Distance) operation rules
1. d(p,q)= 0이면 p=q이다. (역인 p=q이면 d(p,q)=0도 성립한다)
2. d(p,q)= d(q,p)가 성립한다 (교환법칙)
3. d(p,r)<= d(p,q)+ d(q,r)이 성립한다 (피타고라스 법칙)
Similarity rules
similarity(p,q)= s(p,q)로 쓰기로 하자.
1. s(p,q)=1이면 p=q이다. (역인 p=q이면 s(p,q)=1도 성립한다)
2. s(p,q)= s(q,p) 이다. (교환법칙)
Similarity about Binary Vector
두 개의 값(0,1)을 가지는 데이터로 이루어진 벡터의 유사도를 계산할 수도 있다.
감기에 걸린 사람;p= (1,0,0,0.0,0,0)
독감에 걸린 사람;q= (0,0,0,00,0,1)
에서 1은 true, 0은 false를 의미한다고 하자.
M00(p=q=0), M01(p=0, q=1), M10(p=1, q=0), M11(p=q=1) 값을 계산하면 다음과 같다.
=> 해당 케이스에 속하는 쌍의 갯수를 센다
M00= 5
M01= 1
M10= 1
M11= 0
이 때 Simple Matching은 다음과 같이 계산된다.
Simple Matching= (M11+ M00)/(M00+ M01+ M10+ M11)
전체 갯수 중에서 모두 참이거나 모두 거짓인 케이스의 비율
따라서 이 경우 SM= (0+5)/(5+1+1+0)= 0.71..이 된다.
그러나 위의 데이터에서 감기에 걸린 사람과 독감에 걸린 사람 데이터가 높은 유사도(SM= 0.71)가 있다고 보기는 어렵다.
감기에 걸린 사람;p= (1,0,0,0)
독감에 걸린 사람;q= (0,0,0,1)
따라서 SM이 아닌 다른 방법을 사용해볼 수 있다.
Jaccard Coefficients는 다음과 같이 계산한다.
Jaccard Coefficients= M11/(M01+ M10+ M11)
Simple Matching에서 모두 거짓인 값들은 제외하고 계산
J를 계산해보면 0/(1+1+0)= 0이 나온다.
따라서 이 경우 Jaccard Coefficients를 유사도로 사용하는 것이 더 합리적이다.
Documents in Vector Space Model
document(문서)는 수천개의 특정 attribute로 이루어져 있고,
각각은 특정 단어/문단의 출현 빈도로 기록된다.
| 야구 | 팀 | 축구 | |
| 문서1 | 3 | 3 | 0 |
| 문서2 | 0 | 3 | 3 |
위와 같이 N개의 문서를 벡터 데이터로 나타낼 수 있다.
(각 데이터값은 해당 문서의 특정 단어(attribute)출현 횟수)
이 때 차원값은 단어의 수(attribute의 갯수)가 된다.
Cosine Similarity
CS(d1, d2)= d1*d2/||d1||*||d2||로 구할 수 있다.
코사인 유사도는 두 벡터의 벡터곱과, 절댓값을 씌운 각 벡터의 벡터곱의 비율로 나타난다.
다음 document를 벡터로 표현해 보자.
| 야구 | 팀 | 축구 | |
| 문서1 | 3 | 3 | 0 |
| 문서2 | 0 | 3 | 0 |
V(d1)= (3,3,0)
V(d2)= (0,3,3)
d1*d2= (3*0+ 3*3+ 0*0)= 9
||d1||= sqrt(3*3+ 3*3+ 0*0)= 4.24
||d2||= sqrt(0*0+ 3*3+ 0*0)= 3
CS(d1, d2)=9/(4.24*3)= 0.71로 문서1과 문서2의 코사인 유사도는 0.71이다.
유클리드 거리 vs 코사인 유사도
가령 문서1과 문서1의 내용을 복사해 한 권으로 합친 문서 2가 있다고 해 보자.
| 야구 | 팀 | 축구 | |
| 문서1 | 3 | 3 | 0 |
| 문서2 | 6 | 6 | 0 |
이제 d1= (3,3,0), d2= (6,6,0)이 된다.
유클리드 거리d(d1,d2)는 ||d1||=4.24 이 될 것이고
코사인 유사도는 d1*d2= 36, ||d1||= 4.24..., ||d2||= 8.48...이므로, CS(d1,d2)= 1가 되어
실제 두 책의 내용이 양에 차이만 있지 동일한 내용을 담고 있으므로
이 때는 유사도를 관찰할 때 코사인 유사도가 더 적합하다.
'데이터사이언스' 카테고리의 다른 글
| [데이터사이언스] Regression (회귀) (0) | 2021.10.22 |
|---|---|
| [데이터사이언스] 머신러닝 개요 (0) | 2021.10.22 |
| [데이터사이언스] 공분산(Covariance)과 상관관계(Correlation) (0) | 2021.10.21 |
| [데이터사이언스] 데이터 요약과 시각화 (Data summary and visualization) (0) | 2021.10.21 |
| [데이터사이언스] 데이터의 이해 (0) | 2021.10.20 |




